Creating a Range of Numbers as an Array in Numpy using the arange() and linspace() Functions

Introduction

NumPy, short for Numerical Python, is a powerful library for numerical computing in Python. It provides support for large, multi-dimensional arrays and matrices, along with a collection of mathematical functions to operate on these arrays efficiently. NumPy also includes functionalities for generating arrays of numbers, such as evenly spaced range of numbers using functions like arange and linspace, which are essential for various computational tasks. NumPy is widely used in data science, machine learning, scientific computing, and engineering due to its easy handling of complex mathematical operations.

Key Features of NumPy:

1. N-Dimensional Arrays: NumPy introduces the ndarray object, a versatile n-dimensional array that allows efficient storage and manipulation of large datasets.
2. Mathematical Functions: A comprehensive suite of mathematical functions, including statistical, algebraic, and trigonometric operations, is built into NumPy.
3. Broadcasting: This feature allows operations on arrays of different shapes and sizes without the need for explicit loops.
4. Integration with Other Libraries: NumPy serves as the foundation for many other scientific libraries in Python, such as SciPy, Pandas, and Matplotlib.
5. Performance: NumPy operations are implemented in C, making them significantly faster than equivalent Python code, especially for large datasets.

Example:

python
import numpy as np

# Creating a 1D array
array_1d = np.array([1, 2, 3, 4, 5])

# Performing element-wise operations
squared_array = array_1d ** 2

print("Original Array:", array_1d)
print("Squared Array:", squared_array)

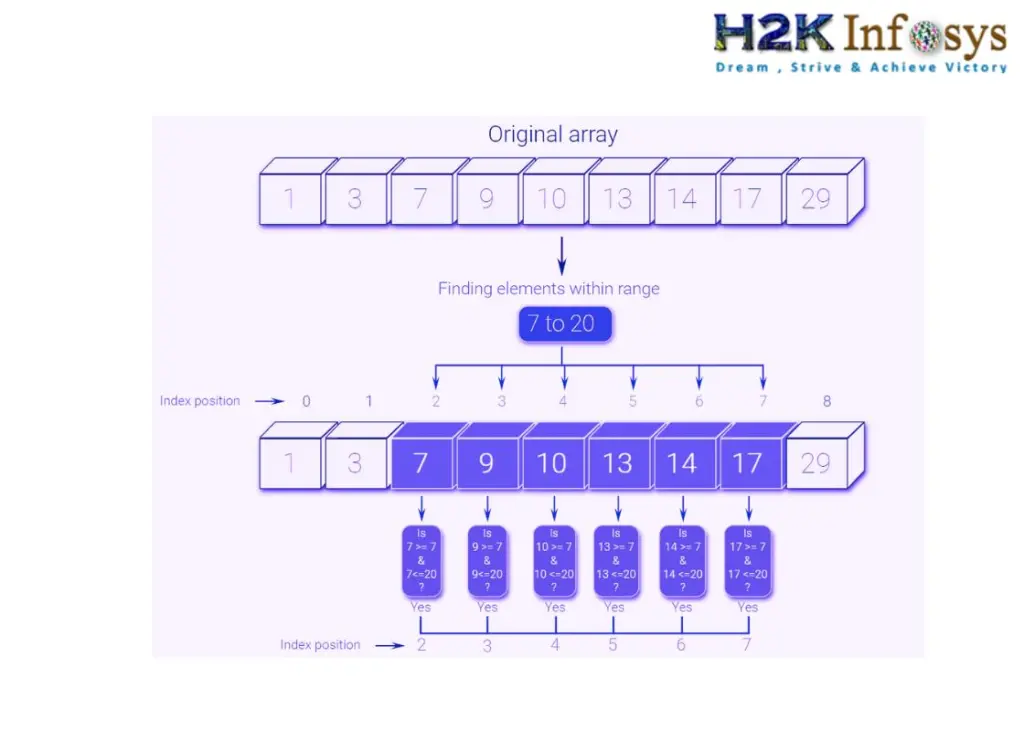
Range of Numbers in NumPy: Importance in Data Analysis and Scientific Computing

Creating ranges of numbers is a fundamental operation in data analysis and scientific computing. NumPy provides efficient ways to generate range of numbers, which are essential for various analytical tasks.

Why Creating Ranges is Useful:

1. Data Preparation: Ranges are often used to create test datasets, initialize variables, or set up configurations for experiments.
2. Indexing and Slicing: Ranges help in selecting specific subsets of data, allowing for efficient data manipulation and analysis.
3. Vectorization: Ranges enable vectorized operations, which are faster and more efficient than traditional looping methods.
4. Simulations and Modeling: In scientific computing, ranges are used to represent time intervals, spatial coordinates, or other continuous variables in simulations and models.
5. Graphing and Visualization: Ranges are crucial for generating the x-axis values in plots and charts, facilitating data visualization.

Examples of Creating Ranges in NumPy:

1. Using arange(): Generates evenly spaced values within a given interval.

python

import numpy as np

# Creating a range from 0 to 10 with a step of 2

range_array = np.arange(0, 10, 2)

print("Range using arange:", range_array)

Using linspace(): Generates a specified number of evenly spaced values between two endpoints.

python

import numpy as np

# Creating 5 values evenly spaced between 0 and 1

linspace_array = np.linspace(0, 1, 5)

print("Range using linspace:", linspace_array)

Using logspace(): Generates values spaced evenly on a log scale.

python

import numpy as np

# Creating 5 values evenly spaced between 10^0 and 10^2

logspace_array = np.logspace(0, 2, 5)

print("Range using logspace:", logspace_array)

Understanding arange() in NumPy

Definition and Purpose: What is arange() and When to Use It

arange() is a function in Python’s NumPy library, which generates arrays with evenly spaced values within a specified range. It is a versatile and efficient tool for creating sequences of numbers, making it fundamental in numerical computing tasks. This function is particularly useful when you need to create arrays for iteration, sampling, or to use as indices in data manipulation tasks.

When to Use arange():

• Iteration: When you need to create a sequence of numbers to loop through.
• Sampling: For generating samples within a specified range.
• Indexing: To create index arrays for slicing or referencing elements in other arrays.
• Mathematical Operations: To generate input values for mathematical functions.

Syntax and Parameters

The syntax of arange() is:

python

numpy.arange([start,] stop[, step,], dtype=None, *, like=None)

Let’s break down each parameter:

1. start (optional): The starting value of the sequence. The default value is 0.
2. stop: The end value of the sequence (exclusive).
3. step (optional): The spacing between values in the sequence. The default value is 1.
4. dtype (optional): The desired data type of the output array. If not specified, it defaults to the data type inferred from the other input arguments.
5. like (optional): Reference object to allow the creation of arrays which are not NumPy array, but are instances of the same type as the provided object.

Detailed Explanation of Each Parameter

1. start:
   • Defines the beginning of the sequence.
   • If omitted, the sequence starts at 0.
   • Example: np.arange(3, 10) starts at 3.
2. stop:
   • Specifies the end of the sequence.
   • The value specified by stop is not included in the sequence.
   • Example: np.arange(3, 10) generates numbers up to, but not including, 10.
3. step:
   • Determines the increment between each value in the sequence.
   • Positive, negative, or fractional values are allowed.
   • Example: np.arange(3, 10, 2) generates the sequence [3, 5, 7, 9].
4. dtype:
   • Specifies the data type of the array elements.
   • Example: np.arange(3, 10, 2, dtype=float) generates the sequence [3.0, 5.0, 7.0, 9.0] with elements of type float.
5. like:
   • Allows creating arrays which are instances of the same class as the provided array-like object.
   • Example: np.arange(3, 10, like=np.array([1,2,3])) ensures the output is of the same array type as the input like parameter.

Basic Examples

Creating a Simple Range of Integers

Example: np.arange(10)

This basic usage generates an array of integers from 0 to 9.

python

import numpy as np

array = np.arange(10)

print(array)

Explanation of Output:

The output is:

csharp

[0 1 2 3 4 5 6 7 8 9]

This array contains 10 integers starting from 0 up to (but not including) 10, with a default step size of 1.

Detailed Examples and Use Cases

Example 1: Specifying Start, Stop, and Step

python

import numpy as np

array = np.arange(2, 20, 3)

print(array)

Explanation:

• start = 2: The sequence starts at 2.
• stop = 20: The sequence stops before 20.
• step = 3: The step size is 3.

Output:

css

[ 2  5  8 11 14 17]

This output shows the sequence starting from 2, incrementing by 3, and stopping before 20.

Example 2: Using Negative Step

python

import numpy as np

array = np.arange(10, 0, -2)

print(array)

Explanation:

• start = 10: The sequence starts at 10.
• stop = 0: The sequence stops before 0.
• step = -2: The step size is -2 (decreasing sequence).

Output:

csharp

[10  8  6  4  2]

The sequence starts at 10 and decrements by 2 until it reaches a value just above 0.

Example 3: Floating Point Steps

python

import numpy as np

array = np.arange(0, 5, 0.5)

print(array)

Explanation:

• start = 0: The sequence starts at 0.
• stop = 5: The sequence stops before 5.
• step = 0.5: The step size is 0.5.

Output:

csharp

[0.  0.5 1.  1.5 2.  2.5 3.  3.5 4.  4.5]

This output demonstrates how arange() can generate a sequence of floating-point numbers with a specified step size.

Example 4: Specifying Data Type

python

import numpy as np

array = np.arange(1, 10, 2, dtype=float)

print(array)

Explanation:

• start = 1: The sequence starts at 1.
• stop = 10: The sequence stops before 10.
• step = 2: The step size is 2.
• dtype = float: The elements are of type float.

Output:

csharp

[1. 3. 5. 7. 9.]

The output sequence contains floating-point numbers instead of integers.

Example 5: Using like Parameter

python

import numpy as np

input_array = np.array([1, 2, 3])

array = np.arange(1, 10, like=input_array)

print(array)

Explanation:

• The like parameter ensures that the output array has the same type as the input array (input_array).

Output:

csharp

[1 2 3 4 5 6 7 8 9]

This ensures that the output array retains the characteristics of the input_array.

Advanced Examples and Considerations

Example 6: Large Ranges

python

import numpy as np

array = np.arange(0, 1000000, 1000)

print(array)

Explanation:

• Generates a large range from 0 to 999,000 with a step of 1,000.

Output:

yaml

[     0   1000   2000 ... 997000 998000 999000]

This example shows arange()‘s capability to handle large ranges efficiently.

Example 7: Handling Overflow

For large ranges with integer overflow:

python

import numpy as np

array = np.arange(1, 1e18, 1e17, dtype=np.float64)

print(array)

Explanation:

• Uses dtype=np.float64 to handle large values.

Output:

csharp

[1.0e+00 1.0e+17 2.0e+17 3.0e+17 4.0e+17 5.0e+17 6.0e+17 7.0e+17 8.0e+17 9.0e+17]

This ensures that the array can hold large numerical values without overflow issues.

Advanced Usage of np.arange()

The np.arange() function in NumPy is a powerful tool for creating arrays with evenly spaced values. Beyond its basic usage, it can handle non-integer steps, negative steps, specified data types, and even complex numbers. Here, we explore these advanced features with examples and explanations.

1. Non-Integer Steps

Creating ranges with floating-point steps

The np.arange() function allows you to create ranges with non-integer steps, which is particularly useful when working with floating-point numbers.

Example:

python

import numpy as np

array = np.arange(0, 1, 0.1)

print(array)

Output:

csharp

[0.  0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9]

Explanation: This example generates an array of values starting from 0 to just below 1, with a step of 0.1. However, due to floating-point precision issues, the end value might not always be included as expected. Floating-point arithmetic can introduce small errors, which means the result might slightly differ from the exact mathematical result.

2. Negative Steps

Creating descending ranges

The np.arange() function can also create arrays in descending order by using a negative step value.

Example:

python

import numpy as np

array = np.arange(10, 0, -1)

print(array)

Output:

csharp

[10  9  8  7  6  5  4  3  2  1]

Explanation: This example generates an array that starts at 10 and decreases to 1, with a step of -1. The function stops just before reaching the end value, creating a descending range of integers.

3. Specifying Data Types

Creating ranges with specific data types

The np.arange() function allows specifying the data type of the resulting array, which can be useful for ensuring consistency in calculations or optimizing memory usage.

Example:

python

import numpy as np

array = np.arange(0, 5, dtype=np.float64)

print(array)

Output:

csharp

[0. 1. 2. 3. 4.]

Explanation: This example creates an array of floating-point numbers from 0 to 4. Specifying the data type as np.float64 ensures that the array elements are 64-bit floating-point numbers. This can be particularly useful when performing scientific computations that require high precision.

4. Complex Numbers

Usage of arange() with complex numbers

The np.arange() function can generate ranges of complex numbers, which is useful in fields like signal processing and electrical engineering.

Example:

python

import numpy as np

array = np.arange(1, 10, 1 + 1j)

print(array)

Output:

csharp

[1. +0.j 2. +1.j 3. +2.j 4. +3.j 5. +4.j 6. +5.j 7. +6.j 8. +7.j 9. +8.j]

Explanation: This example creates an array starting at 1 and ending just before 10, with a step of 1 + 1j. The real part of each subsequent element increases by 1, and the imaginary part also increases by 1, producing a sequence of complex numbers.

Practical Applications of arange()

Indexing and Slicing

arange() is useful for generating indices that can be used for slicing arrays. This allows you to efficiently access and manipulate subsets of your data.

Example: Using arange() to Generate Indices for Slicing

Let’s say you have an array data and you want to select every second element:

python

import numpy as np

data = np.array([10, 20, 30, 40, 50, 60, 70, 80])

indices = np.arange(0, len(data), 2)

sliced_data = data[indices]

print("Original Data:", data)

print("Indices:", indices)

print("Sliced Data:", sliced_data)

Explanation:

• np.arange(0, len(data), 2) generates an array of indices starting at 0, ending before the length of data, and stepping by 2.
• data[indices] uses these indices to slice the data array, resulting in every second element.

Performance Benefits:

• Using arange() to generate indices for slicing can be more efficient than manually creating index arrays, especially for large datasets.
• It avoids the need for loops and enables vectorized operations, which are faster in NumPy due to optimized C and Fortran code under the hood.

Creating Grids

arange() can also be used to create 2D grids, which are useful in various applications such as plotting, simulations, and solving mathematical problems.

Example: Creating 2D Grids with arange()

Let’s create a 2D grid using np.meshgrid():

python

x = np.arange(5)

y = np.arange(5)

X, Y = np.meshgrid(x, y)

print("X Grid:\n", X)

print("Y Grid:\n", Y)

Explanation:

• np.arange(5) creates an array [0, 1, 2, 3, 4] for both x and y.
• np.meshgrid(x, y) generates two 2D arrays:

X contains the x-coordinates, repeated for each row.

Y contains the y-coordinates, repeated for each column.

Output:

less

X Grid:

 [[0 1 2 3 4]

  [0 1 2 3 4]

  [0 1 2 3 4]

  [0 1 2 3 4]

  [0 1 2 3 4]]

Y Grid:

 [[0 0 0 0 0]

  [1 1 1 1 1]

  [2 2 2 2 2]

  [3 3 3 3 3]

  [4 4 4 4 4]]

Use Cases:

• Plotting: Grids are used in contour plots, surface plots, and other visualizations where you need a grid of coordinates.
• Simulations: Grids can represent spatial domains in simulations, such as finite element analysis, fluid dynamics, or heat distribution.
• Mathematical Problems: Solving partial differential equations or optimization problems often requires defining a grid over which calculations are performed.

Range Arguments of np.arange()

The np.arange() function in NumPy is used to create arrays with evenly spaced values within a specified range. This function is versatile and allows you to specify start, stop, and step values.

Providing All Range Arguments

When all three arguments (start, stop, step) are provided to np.arange(), it generates an array starting from ‘start’, incrementing by ‘step’, and stopping before ‘stop’.

Example:

np.arange(1, 10, 2) # Output: array([1, 3, 5, 7, 9])

Providing Two Range Arguments

Example:

By providing two arguments to np.arange(), the function assumes the first argument is the start value and the second is the stop value, with a default step of 1.

np.arange(1, 5) # Output: array([1, 2, 3, 4])

Providing One Range Argument

When only one argument is provided to np.arange(), it is taken as the stop value, and the start value defaults to 0 with a step of 1.

Example:

np.arange(5) # Output: array([0, 1, 2, 3, 4])

Providing Negative Arguments

np.arange() also accepts negative values for start, stop, and step, allowing for the creation of arrays that count backwards or span negative ranges.

Example:

np.arange(-3, 3) # Output: array([-3, -2, -1,  0,  1,  2])

Counting Backwards

To create an array that counts backwards, provide a negative step value. The start value should be greater than the stop value.

Example:

np.arange(5, 0, -1) # Output: array([5, 4, 3, 2, 1])

Getting Empty Arrays

If the provided range arguments do not logically progress from start to stop with the given step, np.arange() will return an empty array.

Example:

np.arange(5, 5) # Output: array([], dtype=int64)

These notes cover the basic usage of np.arange() for creating arrays with different configurations.

Understanding linspace()

Definition and Purpose

numpy.linspace() is a function in the NumPy library used to create an array of evenly spaced numbers over a specified interval? It’s particularly useful in mathematical computations, data analysis, and scientific simulations where you need a sequence of numbers between two endpoints.

Syntax and Parameters

The syntax for numpy.linspace() is:

python

numpy.linspace(start, stop, num=50, endpoint=True, retstep=False, dtype=None, axis=0)

Let’s go through each parameter in detail:

• start:
  • Type: float or array-like
  • Description: The starting value of the sequence.
  • Example: If start=0, the sequence begins at 0.
• stop:
  • Type: float or array-like
  • Description: The end value of the sequence.
  • Example: If stop=1, the sequence will end at or before 1, depending on the value of endpoint.
• num:
  • Type: int, optional (default is 50)
  • Description: The number of samples to generate. This defines how many evenly spaced numbers are in the output array.
  • Example: If num=10, the sequence will have 10 numbers.
• endpoint:
  • Type: boolean, optional (default is True)
  • Description: If True, stop is the last sample. Otherwise, it is not included.
  • Example: If endpoint=False, the sequence will not include the stop value.
• retstep:
  • Type: boolean, optional (default is False)
  • Description: If True, return the step size along with the array.
  • Example: If retstep=True, the function returns a tuple (array, step).
• dtype:
  • Type: dtype, optional
  • Description: The type of the output array. If None, the data type is inferred from the input.
  • Example: If dtype=int, the array elements will be integers.
• axis:
  • Type: int, optional (default is 0)
  • Description: The axis in the result along which the samples are stored. Useful when working with multi-dimensional arrays.
  • Example: If axis=1, samples are stored along the columns of a 2D array.

Basic Examples

Example 1: Creating a Simple Range of Evenly Spaced Numbers

python

import numpy as np

# Create an array of 10 evenly spaced numbers between 0 and 1

array = np.linspace(0, 1, 10)

print(array)

Explanation of Output:

When you run the above code, the output will be:

csharp

[0.         0.11111111 0.22222222 0.33333333 0.44444444 0.55555556

 0.66666667 0.77777778 0.88888889 1.        ]

Here’s the breakdown of what happened:

• start=0: The sequence starts at 0.
• stop=1: The sequence ends at 1.
• num=10: There are 10 numbers in the sequence.
• endpoint=True (default): The stop value (1) is included in the sequence.

The function generated 10 numbers evenly spaced between 0 and 1, inclusive.

Example 2: Using the retstep Parameter

python

import numpy as np

# Create an array and return the step size

array, step = np.linspace(0, 1, 10, retstep=True)

print("Array:", array)

print("Step size:", step)

Explanation of Output:

When you run the above code, the output will be:

vbnet

Array: [0.         0.11111111 0.22222222 0.33333333 0.44444444 0.55555556

 0.66666667 0.77777778 0.88888889 1.        ]

Step size: 0.1111111111111111

Here’s the breakdown of what happened:

• The sequence is the same as in Example 1.
• retstep=True: The function returned the step size (0.1111111111111111) along with the array.

This step size is the difference between each consecutive pair of numbers in the sequence.

By understanding these examples and the parameters of numpy.linspace(), you can effectively generate sequences of evenly spaced numbers for various applications in data analysis and scientific computing.

Advanced Usage of np.linspace()

The np.linspace() function in NumPy is a powerful tool for creating evenly spaced ranges of numbers. It has several advanced features that allow for greater control and flexibility.

1. Specifying Number of Points

Description: You can specify the exact number of points you want in the range.

Example:

python

import numpy as np

result = np.linspace(0, 10, 5)

print(result)

Explanation of Output: This will create an array with 5 evenly spaced numbers between 0 and 10 (inclusive):

css

[ 0.   2.5  5.   7.5 10. ]

The np.linspace(0, 10, 5) function divides the interval from 0 to 10 into 4 equal parts (5 points), including both the start (0) and the end (10).

2. Excluding the Endpoint

Description: You can create a range that excludes the endpoint.

Example:

python

result = np.linspace(0, 1, 10, endpoint=False)

print(result)

Explanation of Use Cases: This will create an array with 10 evenly spaced numbers between 0 and 1, excluding the endpoint 1:

csharp

[0.  0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9]

Excluding the endpoint can be useful when you want to create intervals that do not include the upper limit. For example, this is useful in periodic functions, digital signal processing, or any scenario where the boundary should be open.

3. Returning Step Size

Description: You can get the step size between the points in the range.

Example:

python

result, step = np.linspace(0, 1, 10, retstep=True)

print(result)

print("Step size:", step)

Explanation of Output: This will create an array and also return the step size:

arduino

[0.  0.11111111 0.22222222 0.33333333 0.44444444 0.55555556 0.66666667 0.77777778 0.88888889 1.        ]

Step size: 0.1111111111111111

Returning the step size is useful for understanding the spacing of the points. This is particularly helpful in numerical simulations where the step size needs to be known for further calculations.

4. Specifying Data Types

Description: You can create ranges with specific data types.

Example:

python

result = np.linspace(0, 5, num=5, dtype=np.float64)

print(result)

Explanation of Why This Might Be Useful: This will create an array with 5 evenly spaced floating-point numbers between 0 and 5:

csharp

[0.   1.25 2.5  3.75 5.  ]

Specifying the data type ensures that the generated numbers are in the desired format. This is important in applications where precision is critical, such as scientific computations, financial calculations, or when interfacing with other systems that require a specific data type.

By understanding these advanced usages of np.linspace(), you can leverage its full potential in a variety of scenarios, ensuring precise and flexible numerical operations in your projects.

Practical Applications of linspace()

1. Plotting Functions

Using linspace() for plotting smooth curves:

The linspace() function is highly useful in plotting smooth curves because it generates evenly spaced numbers over a specified range. This is particularly beneficial when you want to create a smooth and continuous plot.

Example: Plotting a sine wave

Here’s an example of how to use linspace() to plot a sine wave.

Code and Explanation:

python

import numpy as np

import matplotlib.pyplot as plt

# Generate 1000 evenly spaced points between 0 and 2π

x = np.linspace(0, 2 * np.pi, 1000)

# Compute the sine of these points

y = np.sin(x)

# Plot the sine wave

plt.plot(x, y)

plt.title("Sine Wave")

plt.xlabel("x")

plt.ylabel("sin(x)")

plt.grid(True)

plt.show()

Explanation:

• np.linspace(0, 2 * np.pi, 1000) generates 1000 points between 0 and 2π2\pi2π.
• np.sin(x) computes the sine of each of these points.
• plt.plot(x, y) creates the plot.
• plt.show() displays the plot.

The result is a smooth sine wave because the points are evenly distributed.

2. Interpolation

Creating ranges for interpolation:

Interpolation involves estimating values between two known values. linspace() helps create a range of values that can be used for interpolation, ensuring that the points are evenly spaced.

Example: Interpolating data points

Here’s how to use linspace() for interpolating between data points.

Code and Explanation:

python

import numpy as np

from scipy.interpolate import interp1d

import matplotlib.pyplot as plt

# Original data points

x = np.array([0, 1, 2, 3, 4, 5])

y = np.array([0, 1, 4, 9, 16, 25])

# Create an interpolation function

f = interp1d(x, y, kind='quadratic')

# Generate new points for interpolation

x_new = np.linspace(0, 5, 50)

y_new = f(x_new)

# Plot original data points

plt.scatter(x, y, color='red', label='Original Data')

# Plot interpolated curve

plt.plot(x_new, y_new, label='Interpolated Curve')

plt.legend()

plt.title("Quadratic Interpolation")

plt.xlabel("x")

plt.ylabel("y")

plt.grid(True)

plt.show()

Explanation:

• np.array([0, 1, 2, 3, 4, 5]) and np.array([0, 1, 4, 9, 16, 25]) are the original data points.
• interp1d(x, y, kind='quadratic') creates an interpolation function.
• np.linspace(0, 5, 50) generates 50 evenly spaced points between 0 and 5 for interpolation.
• f(x_new) computes the interpolated values at these points.
• The plot shows both the original data points and the interpolated curve.

Use Cases:

• Filling in missing data points.
• Creating smooth curves from discrete data points.

3. Creating Grids

Creating 2D grids with linspace():

When dealing with 2D plots or mesh grids, linspace() is essential for creating evenly spaced points along each axis, which can then be used to generate a grid.

Example: Creating a 2D grid

Here’s how to create a 2D grid using np.meshgrid() and linspace().

Code and Explanation:

python

import numpy as np

# Generate 5 evenly spaced points between 0 and 1 for both x and y axes

x = np.linspace(0, 1, 5)

y = np.linspace(0, 1, 5)

# Create a 2D grid

X, Y = np.meshgrid(x, y)

print("X grid:\n", X)

print("Y grid:\n", Y)

Explanation:

• np.linspace(0, 1, 5) generates 5 points between 0 and 1 for both x and y.
• np.meshgrid(x, y) creates two 2D arrays: one for the x-coordinates (X) and one for the y-coordinates (Y).

Output:

less

X grid:

 [[0.   0.25 0.5  0.75 1.  ]

 [0.   0.25 0.5  0.75 1.  ]

 [0.   0.25 0.5  0.75 1.  ]

 [0.   0.25 0.5  0.75 1.  ]

 [0.   0.25 0.5  0.75 1.  ]]

Y grid:

 [[0.   0.   0.   0.   0.  ]

 [0.25 0.25 0.25 0.25 0.25]

 [0.5  0.5  0.5  0.5  0.5 ]

 [0.75 0.75 0.75 0.75 0.75]

 [1.   1.   1.   1.   1.  ]]

Use Cases:

• Visualizing functions of two variables.
• Creating contour plots.
• Performing simulations on a grid.

These examples demonstrate the versatility and utility of linspace() in various practical applications, from plotting functions and interpolating data points to creating grids for 2D visualizations.

linspace in Python

The linspace function in Python, part of the NumPy library, is used to generate an array of evenly spaced numbers over a specified range. It is particularly useful for creating sequences of numbers for mathematical computations and plotting.

Key Features:

• Range Specification: You can define the start and end points of the sequence.
• Number of Points: You specify how many points you want between the start and end.
• Inclusivity: By default, both endpoints are included, but you can exclude the endpoint if needed.

Example:

import numpy as np

# Generate 10 evenly spaced numbers between 1 and 10
numbers = np.linspace(1, 10, 10)
print(numbers)

This will output:

[ 1.  2.  3.  4.  5.  6.  7.  8.  9. 10.]

Usage:

• Plotting: Ideal for creating smooth curves and graphs.
• Simulations: Useful in simulations where a range of values is needed.

The linspace function is a versatile tool for creating numerical ranges efficiently in Python.

Comparing arange() and linspace() in NumPy

arange() and linspace() are two functions in the NumPy library used to generate sequences of numbers. They are similar but have different use cases and properties. Below is a detailed comparison of these functions, including differences in usage, precision, performance, advantages, and disadvantages.

Differences in Usage

arange()

• Syntax: numpy.arange([start, ]stop, [step, ], dtype=None)
• Parameters:

start: The starting value of the sequence (inclusive).

stop: The end value of the sequence (exclusive).

step: The spacing between values (default is 1).

dtype: The data type of the output array (optional).

Example:

python

import numpy as np

# Example: Creating an array from 0 to 10 with a step of 2

arr1 = np.arange(0, 10, 2)

print(arr1)  # Output: [0 2 4 6 8]

linspace()

• Syntax: numpy.linspace(start, stop, num=50, endpoint=True, retstep=False, dtype=None, axis=0)
• Parameters:

start: The starting value of the sequence.

stop: The end value of the sequence.

num: Number of samples to generate (default is 50).

endpoint: If True, stop is the last sample (default is True).

retstep: If True, return the step size (default is False).

dtype: The data type of the output array (optional).

axis: The axis in the result to store the samples (default is 0).

Example:

python

import numpy as np

# Example: Creating an array from 0 to 1 with 5 equally spaced values

arr2 = np.linspace(0, 1, 5)

print(arr2)  # Output: [0.   0.25 0.5  0.75 1.  ]

When to Use arange() vs. linspace()

arange()

• Use arange() when you need to create arrays with a specific step size.
• Best suited for integer sequences or when the step size is an integer.
• Example Scenario: Generating indices for looping or creating a sequence of numbers with a fixed step.

Example:

python

# Generating even numbers between 1 and 10

even_numbers = np.arange(2, 11, 2)

print(even_numbers)  # Output: [2 4 6 8 10]

linspace()

• Use linspace() when you need to create arrays with a specific number of elements.
• Ideal for creating sequences where the start and end values are included, especially for floating-point numbers.
• Example Scenario: Generating values for plotting graphs, where you need a specific number of points between two values.

Example:

python

# Generating 5 points between 0 and 2π for a sine wave

x = np.linspace(0, 2 * np.pi, 5)

y = np.sin(x)

print(x)  # Output: [0.         1.57079633 3.14159265 4.71238898 6.28318531]

print(y)  # Output: [ 0.  1.  0. -1.  0.]

Precision and Performance Differences

Precision

• arange(): May suffer from floating-point precision issues when used with non-integer steps. The accumulation of floating-point errors can lead to unexpected results.
• linspace(): More reliable for generating floating-point sequences as it ensures that the start and end values are included (when endpoint=True).

Performance

• arange(): Generally faster because it computes values using a simple arithmetic progression.
• linspace(): Slightly slower due to additional calculations to ensure equal spacing and inclusion of endpoint values.

Advantages and Disadvantages

arange()

• Advantages:
  • Simple to use for integer sequences.
  • Generally faster due to fewer computations.
• Disadvantages:
  • Can suffer from floating-point precision errors.
  • Less intuitive for generating a specific number of points between a range.

linspace()

• Advantages:
  • Guarantees equally spaced values, including the endpoint.
  • More precise for floating-point ranges.
• Disadvantages:
  • Slightly slower due to more complex calculations.
  • Less intuitive for sequences with a specific step size.

Example Scenarios Highlighting the Best Use Cases

Best Use Case for arange()

Scenario: Creating a sequence of integers for indexing or iteration.

python

# Creating indices for a loop

indices = np.arange(0, 10)

for i in indices:

    print(i)  # Output: 0 1 2 3 4 5 6 7 8 9

Best Use Case for linspace()

Scenario: Generating points for a smooth plot.

python

import matplotlib.pyplot as plt

# Generating 100 points between 0 and 2π

x = np.linspace(0, 2 * np.pi, 100)

y = np.sin(x)

plt.plot(x, y)

plt.xlabel('x')

plt.ylabel('sin(x)')

plt.title('Sine Wave')

plt.show()

In summary, arange() is best for generating sequences with a specified step size, especially for integers, while linspace() is ideal for generating a specified number of equally spaced points between two values, particularly useful in plotting and precise floating-point calculations.

Common Pitfalls and Best Practices in NumPy

Precision Issues: Dealing with Floating-Point Precision in arange()

Explanation:

When using np.arange(), precision issues can arise due to the nature of floating-point arithmetic. np.arange(start, stop, step) generates values from start to stop with a step size of the step. However, small errors can accumulate because floating-point numbers are represented approximately in binary, leading to unexpected results.

Example of Potential Pitfalls:

python

import numpy as np

# Using np.arange with a floating-point step

result = np.arange(0, 1, 0.1)

print(result)

Expected output might be:

csharp

[0.0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9]

However, you might get:

csharp

[0.  0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9]

In some cases, due to floating-point errors, you might see:

csharp

[0.  0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1. ]

Performance Considerations: Performance Comparison Between arange() and linspace()

Explanation:

np.linspace(start, stop, num) generates num evenly spaced samples between start and stop. It is often preferred for generating a fixed number of points with high precision.

Example of Performance Comparison:

python

import numpy as np

import time

# Using np.arange

start_time = time.time()

np.arange(0, 1, 0.0001)

end_time = time.time()

print(f"np.arange took {end_time - start_time} seconds")

# Using np.linspace

start_time = time.time()

np.linspace(0, 1, 10000)

end_time = time.time()

print(f"np.linspace took {end_time - start_time} seconds")

Performance can vary based on the system and conditions, but generally, np.linspace is more consistent in terms of the number of points and precision.

Best Practices:

1. Choosing the Right Function:

• Use np.arange() for integer steps where precision is not a concern.
• Use np.linspace() for floating-point steps and when a specific number of points is required.

2. Writing Clean and Efficient NumPy Code:

Avoid Explicit Loops: Use vectorized operations to leverage NumPy’s performance benefits.

Use Broadcasting: Take advantage of NumPy’s broadcasting rules to write concise and efficient code.

Preallocate Arrays: When working with large arrays, preallocate memory to avoid dynamic resizing.

Use In-Place Operations: Modify arrays in place to reduce memory overhead, e.g., array *= 2 instead of array = array * 2.

Examples of Best Practices:

python

import numpy as np

# Vectorized operation

a = np.array([1, 2, 3, 4, 5])

b = a * 2

# Broadcasting example

a = np.array([1, 2, 3])

b = np.array([[1], [2], [3]])

c = a + b

# Preallocating arrays

n = 10000

preallocated_array = np.empty(n)

for i in range(n):

    preallocated_array[i] = i ** 2

# In-place operations

array = np.array([1, 2, 3, 4, 5])

array *= 2

By understanding these common pitfalls and adopting best practices, you can write more reliable and efficient NumPy code.

Real-World Examples and Case Studies

Scientific Computing

Example: Using linspace() for generating data for scientific simulations

Explanation with Detailed Steps and Code:

The linspace function in NumPy is used to create an array of evenly spaced values over a specified range. This is particularly useful in scientific computing for generating data points for simulations.

Steps:

1. Import the necessary library: Import NumPy.
2. Define the range: Specify the start, end, and the number of points.
3. Generate the data: Use linspace() to generate the data points.
4. Utilize the data: Use the generated data in a simulation or plot it.

Code:

python

import numpy as np

import matplotlib.pyplot as plt

# Step 1: Import the necessary library

import numpy as np

# Step 2: Define the range

start = 0

end = 10

num_points = 100

# Step 3: Generate the data

data_points = np.linspace(start, end, num_points)

# Step 4: Utilize the data

# For example, we can simulate a simple linear function

y = 2 * data_points + 3

Plotting the data

plt.plot(data_points, y)

plt.title('Linear Function Simulation')

plt.xlabel('X values')

plt.ylabel('Y values')

plt.show()

In this example, linspace() generates 100 points between 0 and 10. These points are then used to simulate a linear function y = 2x + 3, which is plotted using Matplotlib.

Data Analysis

Example: Using arange() for indexing and slicing large datasets

Explanation with Detailed Steps and Code:

The arange function in NumPy is used to create arrays with regularly incrementing values. This can be useful for indexing and slicing large datasets.

Steps:

1. Import the necessary library: Import NumPy.
2. Generate an array: Use arange() to create an array of indices.
3. Index and slice the dataset: Use the generated array to index and slice a large dataset.

Code:

python

import numpy as np

import pandas as pd

Step 1: Import the necessary library

import numpy as np

Create a large dataset using pandas

data = pd.DataFrame({

    'A': np.random.rand(1000),

    'B': np.random.rand(1000)

})

Step 2: Generate an array

indices = np.arange(0, 1000, 2)  # Every second index from 0 to 999

Step 3: Index and slice the dataset

sliced_data = data.iloc[indices]

print(sliced_data.head())

In this example, arange(0, 1000, 2) generates an array of even indices from 0 to 999. These indices are then used to slice the dataset, selecting every second row.

Machine Learning

Example: Creating training data ranges with arange() and linspace()

Explanation with Detailed Steps and Code:

In machine learning, you often need to create training data ranges for model training and evaluation. Both arange() and linspace() can be used to generate these ranges.

Steps:

1. Import the necessary library: Import NumPy.
2. Generate data for features and labels: Use arange() or linspace() to create feature ranges.
3. Combine features and labels: Create a dataset for training.

Code:

python

import numpy as np

from sklearn.model_selection import train_test_split

Step 1: Import the necessary library

import numpy as np

Step 2: Generate data for features and labels

X = np.linspace(0, 10, 100).reshape(-1, 1)  # Features

y = 2 * X + 1  # Labels (linear relationship)

Step 3: Combine features and labels (here shown as separate arrays)

Split the dataset into training and testing sets

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

print("Training data:")

print(X_train[:5], y_train[:5])

print("Testing data:")

print(X_test[:5], y_test[:5])

In this example, linspace(0, 10, 100) generates 100 data points between 0 and 10, which are reshaped into a column vector to serve as features. The labels are generated using a simple linear relationship y = 2x + 1. The dataset is then split into training and testing sets using train_test_split from sklearn.

These examples demonstrate how linspace() and arange() can be effectively utilized in scientific computing, data analysis, and machine learning for generating data, indexing, and creating training datasets.

Conclusion

In conclusion, understanding and effectively using these functions in Numpy is crucial for harnessing the full potential of this powerful library. Mastery of Numpy functions allows for efficient data manipulation, comprehensive statistical analysis, and streamlined mathematical operations, all of which are fundamental skills in data science and scientific computing. By investing time in learning and practicing these functions through a Python Online Training Course, you can significantly enhance your ability to process and analyze data, ultimately leading to more insightful and impactful results in your projects.