If you use a smartphone or frequently search the internet, it is highly likely that you have used an application that makes use of a Recurrent Neural Networks (RNN). RNNs are used in speech recognition, language translation, time series forecasting, image captioning etc. In this tutorial, you will learn the following:
- What is a Recurrent Neural Networks?
- Difference between Artificial Neural Networks and RNNs
- How RNNs work
- Types of RNNs
- How to implement a simple RNN model
- Variants of RNNs
What is an RNN?
RNNs are neural networks that are good at modelling sequential data due to the ability to retain memory about a sequence. Sequential data refers to data such as text whose sequence is important for it to have meaning.
RNNs vs Artificial Neural Networks (ANNs)
With ordinary Artificial Neural Networks or even Convolutional Neural Networks (CNNs), the structure is simple and relies on matrix multiplication.
We have the input (x), weights (w), and bias (b). In the hidden layer, the input is multiplied by the weights and the bias is added, i.e.
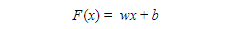
An activation function for example a sigmoid activation function or relu is then used to transform the output of the above calculation into a value that is used to make a prediction, which is the output (y), i.e.
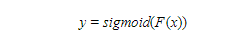
We can have multiple layers inside the hidden layer which perform these calculations from one layer to the next. The last layer then gives the output of the network. The predictions at this first run through the network are usually very far from the actual outcomes. A loss function is applied, which calculates the difference between the predicted values and the actual true values. This result is then used to go back into the network, in a process called backpropagation, and update the weights. This process is done iteratively until the loss is minimized. A simple artificial neural network can be illustrated by the following:
This works well for data that has features that do not depend on each other. For an application such as fruit classification, we might need the shape, colour, size etc. of a fruit in order to classify it. It can be observed that these features are independent of each other. We know that shape does not depend on colour, colour does not depend on size and so on. A neural network can therefore be used in such cases.
However, in a case such as language translation where the order of words in a sentence or phrase matters, it can be observed that some of the features depend on each other. Therefore, there is a need to have some form of memory in order to remember the words that came before a particular word in a sentence.
RNNs are good at processing sequential data because they have ‘sequential memory.’ Let’s take an example of the input sentence ‘the food is ready’. RNNs have a looping mechanism that is used to remember the words that came before each word in the sentence. A simple RNN can be illustrated by the following:
This is a ‘rolled’ illustration of the RNN. To understand it better, we can ‘unroll’ it and show the steps of the looping mechanism:
This is a visualization for your understanding. An unrolled network is represented as follows:
How it works
We have established that an RNN has a looping mechanism that retains memory. Now, we have the question, how does it do this?In an ANN, the weights and bias in the hidden layers are different and independent of each other. In an RNN, they are dependent on each other. The RNN gives the same weights and bias to all layers in the hidden layer and uses the output of each layer as input to the next layer. So, the multiple layers can be combined into one recurrent layer. In order to obtain the current state in an RNN at any time (t), we have
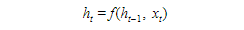
where ht is the current state, ht-1 is the previous state and xt is the input. We can observe that the mechanism relies on a simple loop from one time point to the next. Each time step relies on the input from the previous time step.
It is important to note that at each step, the RNN remembers less and less of the beginning of the sequence, i.e. it has short term memory. Therefore, it might encounter challenges with very long sequences.
Types of Recurrent Neural Networks
Unlike feed forward ANNs that map an input to one output, RNNs have inputs that can vary in length and the outputs can also vary in length. The application of the RNN determines its structure.
One-to-One
Let’s take each circle to represent a vector and arrows to represent functions e.g. (F(x)). The hidden layer vectors hold the RNN’s state. In a One-to-One RNN, we have a fixed size input and a fixed size output. This is basically an ANN. We can apply this in image classification, the fruit classification example we discussed earlier etc.
One-to-Many
In this case, we have a fixed size input and a sequence output. The sequence can vary in size. An application of this image captioning. An image is input and a sentence or phrase is output. If you have ever used an application like Instagram with a poor internet connection, you might have seen some image captions on your timeline instead of photos.
Many-to-One
We can have a sequence input and a fixed size output. Note that the sequence can vary in length. An application of this is sentiment analysis, where we have a sequence input and the output is a fixed value which shows whether the sentiment is positive, negative or neutral.
Many-to-Many
We can have synced sequential input and output. An application of this is video classification, where each frame of the video has to be labelled.
Many-to-Many
We can also have sequence input and sequence output that is not synced. An application is in language translation where a sequence in a language e.g. French is input and the output is a sequence in another language e.g. Spanish.
Let’s implement a simple RNN
In this section, we are going to implement a simple Recurrent Neural Networks RNN model to predict the cosine series. We first create the dataset of values of the cosine of 3000 numbers in the range 1 to 100:
cos_wave = np.array([math.cos(x) for x in np.linspace(1, 100, 3000)])
Now that we have the series, we want to define the training dataset. We choose a sequence of length 500, i.e. given a sequence of 500 numbers in the series, it predicts the number after the 500th term. Therefore, each Yi value corresponds to a sequence, Xi, of 500 numbers in the series.
X = [] Y = [] seq_len = 500 #sequence length num_records = len(cos_wave) - seq_len for i in range(num_records - 500): X.append(cos_wave[i:i+seq_len]) Y.append(cos_wave[i+seq_len]) X = np.array(X) X = np.expand_dims(X, axis=2) Y = np.array(Y) Y = np.expand_dims(Y, axis=1)
The above code selects the training set. An RNN takes 3-dimensional input. This is the reason why we have the line X = np.expand_dims(X, axis=2) which expands the shape of X to a 3-dimensional shape.
The following code defines the validation dataset.
#validation data X_val = [] Y_val = [] for i in range(num_records - 500, num_records): X_val.append(cos_wave[i:i+seq_len]) Y_val.append(cos_wave[i+seq_len]) X_val = np.array(X_val) X_val = np.expand_dims(X_val, axis=2) Y_val = np.array(Y_val) Y_val = np.expand_dims(Y_val, axis=1)
Now, we create the model. The model has an input layer of the same size as each Xi example, i.e. 500. We have the RNN layer and the output layer. This is an example of a many-to-one RNN.
def network(): model = Sequential() model.add(keras.layers.InputLayer(input_shape=(X.shape[1],1))) model.add(keras.layers.recurrent.SimpleRNN(units = 200, activation='linear', use_bias=True)) model.add(keras.layers.Dense(units=1, activation='linear')) model.compile(loss='mean_squared_error', optimizer='adam', metrics=['mse']) return model
We now compile the model:
#compiling the model model = network() model.fit(X, Y, epochs=10, batch_size=100,validation_data=(X_val, Y_val))
We then make predictions using validation data and plot the actual curve (in red) and predicted curve (in green):
fig, ax = plt.subplots(2, 1, sharex=True, figsize=[12,8])
ax[0].plot(val_prediction, 'g')
ax[0].set_title('Prediction')
ax[1].plot(Y_val, 'r')
ax[1].set_title('Real')
The RNN does a fairly good job of predicting the values in the series. You can try with more complex datasets such as text and see the results.
Variants of RNNs
RNNs face some challenges, particularly vanishing gradients and exploding gradients which cause computation to be slow. When performing backpropagation, the idea is to minimize the loss and when using the gradient descent technique, it means the gradient has to keep decreasing as the algorithm iterates. RNNs’ mechanism includes multiple iterations and this is prone to the gradient becoming zero i.e. vanishing. This is the vanishing gradient problem. The algorithm encounters a challenge in such a case as there is no way forward. RNNs also have short term memory so they have difficulty when the sequences are very long. They also do not consider future input but only past input for the current state. Variants of RNNs have been developed which address some of the problems.
Bidirectional RNNs (BRNNs)
We mentioned that RNNs do not consider future input of a current state. BRNNs address this challenge. They have the ability to pull in future input from a sequence. This is useful especially for text, where sometimes it is easier to predict a word when the word that comes after it is known.
Long short-term memory (LSTM)
LSTMs are very popular and were introduced as a solution to the vanishing gradients problem. They have the ability to keep gradients steep, therefore keeping the training short. They are able to retain memory over longer periods of time. They have a gated cell mechanism that allows them to decide whether to keep certain information from the previous input or to discard/”forget” it. The hidden state of an LSTM contains 3 gates, the input, forget and output gates, which are used to decide whether to allow new input in, forget it or let it affect the output of the current state.
Gated Recurrent Units (GRUs)
GRUs are similar to LSTMs. They address the problem of short term memory that is faced by RNNs. The difference with LSTMs is that GRUs use hidden states instead of cell states to regulate information. They also use 2 gates instead of 3. The 2 are the reset gate and update gate. They work the same as in LSTMs.
Conclusion
RNNs remember information through time which is useful in applications such as time series predictions and language translation. However, they also face challenges as they have short term memory and are prone to the problems of exploding gradients and vanishing gradients. Variants of RNNs have become useful in solving these challenges and can be used for more complex problems. I hope you found this tutorial interesting and can work on a problem requiring an RNN as a solution!