In the previous article, we have seen the basic concepts and basic terminology in statistics. Now we are going to learn about some important statistics concepts for data science
Important Statistics Concepts for Data Science
In order to become a fabulous data scientist, you need to know these important statistics concepts. These are the basic statistical concepts that will come in handy for any data scientist.
Measures of Variability
A measure of variability is a summary statistic that represents the amount of dispersion in a dataset and how it is spread out across the values.
While a measure of central tendency describes the typical value, measures of variability define how far away the data points tend to fall from the center. We talk about variability in the context of a distribution of values. A low dispersion indicates that the data points tend to be clustered tightly around the center. High dispersion signifies that they tend to fall further away
The most common measures of variability are
- Range
- Interquartile range (IQR)
- Variance
- Standard Deviation.
Range
Let’s start with the range because it is the most straightforward measure of variability to calculate and the simplest to understand. The range is the difference between the largest and smallest values in a set of values.
Consider the following numbers: 1, 3, 4, 5, 5, 6, 7, 11
11 – 1 = 10 is the Range
While the range is easy to understand, it is based on only the two most extreme values in the dataset, which makes it very susceptible to outliers. If one of those numbers is unusually high or low, it affects the entire range even if it is atypical. So we should use the range to compare variability only when the sample sizes are similar.
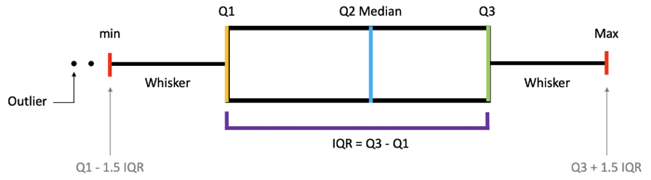
Interquartile range (IQR)
In order to understand IQR better, we need to know what Percentiles and Quartiles are
- Percentiles: A measure that indicates the value below which a given percentage of observations in a group of observations falls.
- Quantiles: Values that divide the number of data points into four more or less equal parts, or quarters.
Interquartile range (IQR) is a measure of variability, based on dividing a data set into quartiles. Quartiles divide a rank-ordered data set into four equal parts.
The values that divide each part are called the first, second, and third quartiles; and they are denoted by Q1, Q2, and Q3, respectively.
• Q1 is the “middle” value in the first half of the rank-ordered data set.
• Q2 is the median value in the set.
• Q3 is the “middle” value in the second half of the rank-ordered data set.
The interquartile range is equal to Q3 minus Q1. For example,
consider the following numbers
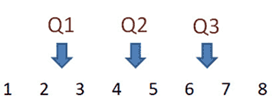
The median is equal to the average of the two middle values.
Q2 = (4 + 5)/2 or Q2 = 4.5.
Since there are an even number of data points in the first half of the data set, the middle value is the average of the two middle values; that is,
Q1 = (2 + 3)/2 or Q1 = 2.5
Again, since the second half of the data set has an even number of observations, the middle value is the average of the two middle values; that is,
Q3 = (6 + 7)/2 or Q3 = 6.5.
The interquartile range is
Q3 – Q1, so IQR = 6.5 – 2.5 = 4.
Variance
In a population, the variance is the average squared deviation from the population mean
σ2 = Σ ( Xi – μ )2 / N
- Sample variance: It defined by slightly different formula, and uses a slightly different notation:
s2 = Σ ( xi – x )2 / ( n – 1 )
Standard deviation
In statistics, the standard deviation is a measure of the amount of variation or dispersion of a set of values. A low standard deviation indicates that the values tend to be close to the mean of the set, while a high standard deviation indicates that the values are spread out over a wider range.
The standard deviation of a population
σ = sqrt [ σ2 ] = sqrt [ Σ ( Xi – μ )2 / N ]
The standard deviation of a Sample
s = sqrt [ s2 ] = sqrt [ Σ ( xi – x )2 / ( n – 1 ) ]
- z-Scores: A z-score / standard score indicates how many standard deviations an element is from the mean
- z = (X – μ) / σ
- A z-score < 0 represents an element less than the mean.
- A z-score > 0 represents an element greater than the mean.
- A z-score = 0 represents an element equal to the mean.
- A z-score equal to 1 represents an element that is 1 standard deviation greater than the mean
- A z-score equal to -1 represents an element that is 1 standard deviation less than the mean
- z = (X – μ) / σ
Measurements of Relationships between Variables
It statistical measures which show a relationship between two or more variables or two or more sets of data. For example, generally, there is a high relationship between a person’s education and academic achievement. On the other hand, there is generally no relationship between a person’s height and academic achievement
These are the commonly used methods to find the relationship between the variables
- Causality
- Covariance
- Correlation
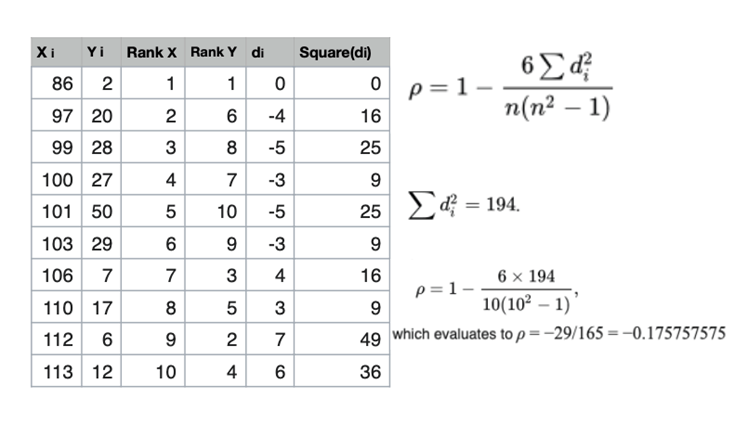
- Spearman’s rank correlation coefficient
Causality
It is influence by which one event, process, or state (a cause) contributes to the production of another event, process, or state where the cause is partly responsible for the effect, and the effect is partly dependent on the cause.
Covariance
It is a measure of how much two random variables vary together. It’s similar to variance, but where variance tells you how a single variable varies, covariance tells you how two variables vary together.
- Positive covariance. Indicates that two variables tend to move in the same direction.
- Negative covariance. Reveals that two variables tend to move in inverse directions.
Covariance for population Covariance for Samples

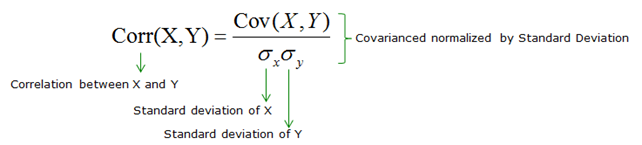
Pearson Correlation
The Pearson correlation between the two variables is a normalized version of the covariance.
Once we’ve normalized the metric to the -1 to 1 scale, we can make meaningful statements and compare correlations.
Spearman’s rank correlation coefficient
The Spearman correlation between two variables is equal to the Pearson correlation between the rank values of those two variables; while Pearson’s correlation assesses linear relationships, Spearman’s correlation assesses monotonic relationships (whether linear or not). If there are no repeated data values, a perfect Spearman correlation of +1 or −1 occurs when each of the variables is a perfect monotone function of the other