Supervised machine learning problems can be broadly divided into 2: Regression problems and classification problems.
In the previous tutorials, we have examined how to build a linear regression model with Tensorflow and Keras. In this tutorial, we shall be turning our attention to classification problems. Classification problems take a large chunk of machine learning problems. Thus, It is critically important to understand how to build classifiers using machine learning algorithms or deep learning techniques.
Later in this tutorial, we will build a linear classifier using Tensorflow Keras. We’d begin by brushing up on all the theoretical concepts of linear classifiers before going ahead to build one.
By the end of the tutorial, you’d discover:
- What is a Linear Classifier?
- Types of Classification Problems
- The Workings of a Binary Classifier
- How the Performance of a Binary Classifier is Measured
- Exploratory Data Analysis (EDA)
- Checking for imbalanced dataset
- Checking for Correlation
- Data Preprocessing
- Building a Single Layer Perceptron for binary classification
- Building a Multilayer Perceptronfor binary classification
What is a Linear Classifier?
To answer this, we need to first understand what a classifier is. A classifier is a model that predicts the class of an object, given its properties. For instance, if my model determines whether an object is a cat or a dog, that is a classifier. In classification problems, the labels, which are called classes, are discrete rather than continuous numbers in regression problems.
Basically, a classifier splits the observations into its class. But while this splitting can be done using a straight hyperplane, some datasets may contain class boundaries that cannot be split by a straight hyperplane. A model in which the classification cannot be done with a hyperplane is called a nonlinear classifier. A linear classifier on the other hand is a model that can capture the class boundaries using straight lines or hyperplanes.
Types of Classification Problems
Classification problems can also be divided into three based on the label classes – binary classification, multiclass classification, and multilabel classification
- Binary classification problem: This is a classification problem where the label contains only two classes. For instance, a model that predicts whether an individual has COVID-19 or not. Or a model that determines whether mail is spam or not.
- Multiclass classification problem: In this type of classification problem, the label contains more than 2 classes. For example, the popular iris dataset contains 3 classes (iris setosa, iris virginica, and iris Versicolor). Such a classification problem is called a multiclass classification problem.
- Multilabel classification problems: For this kind of classification problem, each label class would have more than a class. In photo recognition problems, there may be more than one object in the picture, maybe a dog, and a house. Therefore, the model would predict more than one class for this photo. This is a typical multilabel classification problem.
In this tutorial, we shall build a binary classifier. Let’s understand how it works
The Workings of a Binary Classifier
In supervised learning, the dataset comprises independent variables (called features) and dependent features (called labels). For linear regression problems which we treated in the last tutorial, the variables are continuous numbers (any real number). In such cases, the model attempts to predict the exact number and checks its success by determining how close it is to the correct number. Metrics such as root mean square error, r-squared error, or mean absolute error are common metrics to check how well the model has performed.
For binary classification problems, the labels are two discrete numbers, 1(yes) or 0 (no). The classifier predicts the probability of the occurrence of each class. It then returns the class with the highest probability. Logistic regression is typically used to compute the probability of each class in a binary classification problem. But how does the logistic regression work?
A Logistic Function
Logistic regression makes use of the logistic function (called a sigmoid function) to return a class output. The function is an S-curve that receives any continuous number and maps it within the range of 0 to 1 (although not exactly equal to 0 or 1).
The function is given as
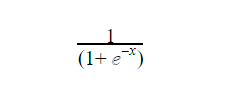
Where x is the continuous number that would be transformed into a number between 0 and 1. The graph is typically in this form
Where x is the continuous number that would be transformed into a number between 0 and 1. The graph is typically in this form
Source: TowardsDataScience
The Logistic Regression Equation
In logistic regression, the independent variables (x) alongside some assigned weights (b) are used to predict the binary outputs (y). The linear regression equation is given below.
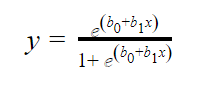
Where b0 is the bias, b1 is the weight of each independent variable (x). The weight shows how the independent variables (x) are correlated with the dependent variable (y). Hence, a positive correlation causes an increase in the probability of the positive while a negative correlation does otherwise.
Once the output of the equation is found, the logistic function converts them into probabilities.
How the Performance of a Binary Classifier is Measured
You’d need to check how well your binary classifier is performing having built it. There are a couple of metrics to check your classifier performance. Let’s talk about the most popular ones.
- Accuracy
Accuracy is perhaps the simplest and commonest metrics. It is simply the ratio of the total number of correct predictions to the total number of predictions made. For example, in a dataset of 1000 samples with labels indicating whether a mail is a spam or ham. If the model makes 850 correct predictions, the accuracy is simply 850 / 1000 which is 85%.
Making use of accuracy has some shortcomings, however. In an unbalanced dataset using accuracy can be misleading. An unbalanced dataset is one where the occurrence of one class far outweighs the occurrence of the other. In the earlier instance I gave, imagine the labels have 850 labels that belong to ham and 150 that belong to spam. This is an example of an imbalanced dataset since 850 outweighs 150 by a large margin.
If we build a dummy model that predicts that all observations are a ham without checking the independent features. The model would still have an accuracy of 85%. This is intrinsically not a good
metric to use for such data. Furthermore, accuracy does not take into account the probability of each class. This may also be a bottleneck when you wish to finetune the outputs of the model for better results.
- Confusion Matrix
The confusion matrix is another popular metric for binary classification problems. The matrix is divided into four quadrants: true positive (TP), false positive (FP), true negative (TN), false negative (FN). Let’s see what the confusion matrix looks like then explain what these terms mean.
Source: Packt
As seen above, the row indicates the actual value and the column indicates the predicted values. The 4 quadrants are the interception of the actual and predicted values.
TN: This is when the model predicts that observation is NOT a class and is actually correct. Say, the model predicts that observation is not spam, and is correctly so.
FN: This is when the model predicts that observation is NOT a class but is incorrect. Say, the model predicts that observation is not spam, but it is actually spam.
FP: This is when the model predicts that an observation is a class but is incorrect. Say, the model predicts that observation is spam, but it is actually not spam.
TP: This is when the model predicts that an observation is a class and it actually is correct. Say, the model predicts that observation is spam and is correctly so.
The confusion matrix adds a lot of flexibility to the performance measure and birth concepts such as precision and recall.
- Precision: The precision indicates how accurate the positive class is. Mathematically, the precision is given by
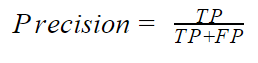
If the model correctly predicts all positive classes, the precision will be equal to 1. This is not a very good metric, especially for an unbalanced dataset with a high positive class, since the precision neglects the negative classes. It can however be useful when we place grave importance on the positive class. An example would be the ham(P)/spam(N) classifier. In this problem, the major concern is to correctly predict that spam is spam (TP) while not predicting a ham as spam. Predicting a ham when it is actually spam (FN) may not have serious consequences but predicting a ham as spam (FP) can be very expensive. You have a high precision when the TP is high and the FP is low.
Precision is typically combined with another metric called the recall.
- Recall: Recall is basically concerned about the rate of positive classes that was predicted corrected. It is also called the sensitivity of true positive rate. Mathematically, the recall is given by
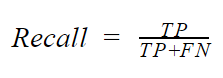
The recall is particularly important in situations where the true positive is critically important such as a cancer classifier. In such a situation, predicting that a patient has cancer when he does not have cancer may not be severe. However, predicting that a patient does not have cancer when they actually do (FN), can be very grave. In situations such as this, it is critically important to check the recall of your model. This is because to get a high recall, the FN must be, low.
- F1 score
F1 score takes both the recall and precision into cognizance. Mathematically, the f1 score is given by
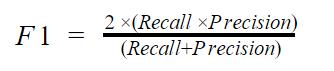
If you are looking for a balance between recall and precision, you should go for the F1 score.
Building a Binary Classifier with Keras on Tensorflow
IN this section, we will go-ahead to build a binary classifier using Keras. The dataset used is the dataset from the National Institute of Diabetes and Digestive and Kidney Diseases. The dataset shows whether or not a patient has diabetes based on some diagnostic measurements such as age, glucose level, blood pressure, insulin level, and so on. We will begin by importing the data using the pandas read_csv() method. We will then check out how the data frame looks like by printing the first five rows.
#import necessary libraries
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.model_selection import train_test_split
import tensorflow as tf
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense, Dropout
#read the dataset file
df = pd.read_csv('diabetes.csv')
#print the first five rows of the dataframe
print(df.head())Output:
Pregnancies Glucose BloodPressure SkinThickness Insulin BMI \ 0 6 148 72 35 0 33.6 1 1 85 66 29 0 26.6 2 8 183 64 0 0 23.3 3 1 89 66 23 94 28.1 4 0 137 40 35 168 43.1 DiabetesPedigreeFunction Age Outcome 0 0.627 50 1 1 0.351 31 0 2 0.672 32 1 3 0.167 21 0 4 2.288 33 1
Exploratory Data Analysis (EDA)
It is important to know the numbers of rows in your dataset. That way, you’d be able to determine how large or small your data is.
df.shape
Output:
(768, 9)
So as shown above, the dataset has 768 rows with 9 columns (including the target column). This is thus a fairly small dataset. Let’s get some more information about each column.
#check the datatype of each column df.info()
Output:
<class 'pandas.core.frame.DataFrame'> RangeIndex: 768 entries, 0 to 767 Data columns (total 9 columns): Pregnancies 768 non-null int64 Glucose 768 non-null int64 BloodPressure 768 non-null int64 SkinThickness 768 non-null int64 Insulin 768 non-null int64 BMI 768 non-null float64 DiabetesPedigreeFunction 768 non-null float64 Age 768 non-null int64 Outcome 768 non-null int64 dtypes: float64(2), int64(7) memory usage: 54.1 KB
All columns are of int data type except for BMI and Diabetes Pedigree Function that are of data type float64. The info() method also revealed that all columns contain non-null values. We can however confirm this by using the isnull() method.
#check for null values df.isnull().sum()
Output:
Pregnancies 0 Glucose 0 BloodPressure 0 SkinThickness 0 Insulin 0 BMI 0 DiabetesPedigreeFunction 0 Age 0 Outcome 0 dtype: int64
Next, we would use the describe method to get the statistical details for each column.
#print the statistical summary for each column df.describe()
Output:
Pregnancies Glucose BloodPressure SkinThickness Insulin \ count 768.000000 768.000000 768.000000 768.000000 768.000000 mean 3.845052 120.894531 69.105469 20.536458 79.799479 std 3.369578 31.972618 19.355807 15.952218 115.244002 min 0.000000 0.000000 0.000000 0.000000 0.000000 25% 1.000000 99.000000 62.000000 0.000000 0.000000 50% 3.000000 117.000000 72.000000 23.000000 30.500000 75% 6.000000 140.250000 80.000000 32.000000 127.250000 max 17.000000 199.000000 122.000000 99.000000 846.000000 BMI DiabetesPedigreeFunction Age Outcome count 768.000000 768.000000 768.000000 768.000000 mean 31.992578 0.471876 33.240885 0.348958 std 7.884160 0.331329 11.760232 0.476951 min 0.000000 0.078000 21.000000 0.000000 25% 27.300000 0.243750 24.000000 0.000000 50% 32.000000 0.372500 29.000000 0.000000 75% 36.600000 0.626250 41.000000 1.000000 max 67.100000 2.420000 81.000000 1.000000
Checking if the data is imbalanced
When dealing with binary classification problems, this is an important step. If an imbalanced dataset is fed into a machine learning model, the model tends to perform lowers. Let’s see whether our data is imbalanced. We use seaborn’s countplot() method. This method counts the occurrence of each class in a column and plots a simple bar graph.
#plot a bar plot that shows the number of each class labels sns.countplot(df['Outcome'])
Output:
You get insight by plotting a bivariate graph for the columns using the Pairplot method of seaborn.
#make a plot of the columns against one another sns.pairplot(df, hue='Outcome')
Output:
From the plot, you’d notice that classes are separable by using a hyperplane (or line) to split the data
Checking for Correlation
As a way of exploring your data, you should check for data correlation. This gives you insight as to what attribute after the other and the way they are connected. Harmed with this knowledge, you could drop or merge columns to reduce the dimensionality of the data. A strong correlation can also give you an idea of what to replace missing values with. Let’s check if some columns are strongly correlated. We use the corr() method and then draw a heat map.
#check the correlation of each column plt.figure(figsize=(10, 6)) sns.heatmap(df.corr(), cmap='Blues', annot=True)
Output:
Split the Data into Train and Test Data
As we gear up to build the deep learning model, we need to split the data into train and test data. Before that, the data needs to be split into its independent variable(X) and dependent variable (y). The independent variables are simply the data without the label column. Hence, we drop that column. The dependent variable on the other hand is the label column alone.
Afterward, the X and y data and split into train and test datasets. Given that the test data is 20% of the entire data. If you do not understand why the data is split into train and test. See the test data has a portion of the data that is hidden from the model during training. It is then used to measure how well the model will predict unseen data.
#split the data into features and labels X = df.drop(['Outcome'], axis=1) y = df['Outcome'] #further split the labels and features into train and test data X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=1)
Checking for Outliers
As explained in the previous tutorial, outliers can affect how the models perform. Thus, it is pivotal to check for them and deal with them. Here, we will graph the boxplot for each column to detect the presence of outliers.
#create a copy of the dataset df1 = df.copy() # # Create a figure with 10 subplots with a width spacing of 1.5 fig, ax = plt.subplots(2,3) fig.subplots_adjust(wspace=1.5) # Create a boxplot for the continuous features box_plot1 = sns.boxplot(y=np.log(df1[df1.columns[0]]), ax=ax[0][0]) box_plot2 = sns.boxplot(y=np.log(df1[df1.columns[1]]), ax=ax[0][1]) box_plot3 = sns.boxplot(y=np.log(df1[df1.columns[2]]), ax=ax[0][2]) box_plot6 = sns.boxplot(y=np.log(df1[df1.columns[5]]), ax=ax[1][0]) box_plot7 = sns.boxplot(y=np.log(df1[df1.columns[6]]), ax=ax[1][1]) box_plot8 = sns.boxplot(y=np.log(df1[df1.columns[7]]), ax=ax[1][2]) ;
Output:
You’d notice that Glucose, BloodPressure, and BMI have sprinkles of outliers. The effect of these data points can be softened by standardizing the data.
Building the Neural Network (a Single Layer Perceptron)
We will begin by building a simple neural network – one fully connected hidden layer with the same number of nodes, as the independent variables (8). This is a neutral way to begin building neural networks. The ReLu activation function is used for the input layer. The outer layer is a single node that spits out the probability of the output class. Hence, a sigmoid activation function is used. This probability can be easily converted into class values.
Furthermore, the common binary_crossentropy is used as the loss function. This the preferable loss function for classification problems. Adam optimizer is used for the gradient descent optimization. Finally, accuracy, precision and recall are set as the model’s metrics.
def create_model(): '''The function creates a Perceptron using Keras''' model = Sequential() model.add(Dense(8, input_dim=len(X.columns), activation='relu')) model.add(Dense(1, activation='sigmoid')) return model estimator = create_model() estimator.compile(optimizer='adam', metrics=['accuracy', tf.keras.metrics.Precision(), tf.keras.metrics.Recall()], loss='binary_crossentropy')
The model is then trained on the train dataset, specifying the test datasets as the validation data.
#train the model history = estimator.fit(X_train, y_train, epochs=300, validation_data=(X_test, y_test))
Output:
Train on 614 samples, validate on 154 samples Epoch 1/300 614/614 [==============================] - 3s 5ms/sample - loss: 0.6690 - acc: 0.6531 - precision_14: 0.0000e+00 - recall_14: 0.0000e+00 - val_loss: 0.6787 - val_acc: 0.6429 - val_precision_14: 0.0000e+00 - val_recall_14: 0.0000e+00 Epoch 2/300 614/614 [==============================] - 0s 168us/sample - loss: 0.6657 - acc: 0.6531 - precision_14: 0.0000e+00 - recall_14: 0.0000e+00 - val_loss: 0.6754 - val_acc: 0.6429 - val_precision_14: 0.0000e+00 - val_recall_14: 0.0000e+00 Epoch 3/300 614/614 [==============================] - 0s 173us/sample - loss: 0.6622 - acc: 0.6531 - precision_14: 0.0000e+00 - recall_14: 0.0000e+00 - val_loss: 0.6729 - val_acc: 0.6429 - val_precision_14: 0.0000e+00 - val_recall_14: 0.0000e+00 Epoch 4/300 614/614 [==============================] - 0s 163us/sample - loss: 0.6600 - acc: 0.6531 - precision_14: 0.0000e+00 - recall_14: 0.0000e+00 - val_loss: 0.6713 - val_acc: 0.6429 - val_precision_14: 0.0000e+00 - val_recall_14: 0.0000e+00 Epoch 5/300 614/614 [==============================] - 0s 166us/sample - loss: 0.6572 - acc: 0.6531 - precision_14: 0.0000e+00 - recall_14: 0.0000e+00 - val_loss: 0.6689 - val_acc: 0.6429 - val_precision_14: 0.0000e+00 - val_recall_14: 0.0000e+00 Epoch 6/300 614/614 [==============================] - 0s 164us/sample - loss: 0.6547 - acc: 0.6531 - precision_14: 0.0000e+00 - recall_14: 0.0000e+00 - val_loss: 0.6663 - val_acc: 0.6429 - val_precision_14: 0.0000e+00 - val_recall_14: 0.0000e+00 Epoch 7/300 614/614 [==============================] - 0s 229us/sample - loss: 0.6524 - acc: 0.6531 - precision_14: 0.0000e+00 - recall_14: 0.0000e+00 - val_loss: 0.6645 - val_acc: 0.6429 - val_precision_14: 0.0000e+00 - val_recall_14: 0.0000e+00 Epoch 8/300 614/614 [==============================] - 0s 214us/sample - loss: 0.6504 - acc: 0.6547 - precision_14: 1.0000 - recall_14: 0.0047 - val_loss: 0.6626 - val_acc: 0.6429 - val_precision_14: 0.0000e+00 - val_recall_14: 0.0000e+00 Epoch 9/300 614/614 [==============================] - 0s 161us/sample - loss: 0.6483 - acc: 0.6547 - precision_14: 1.0000 - recall_14: 0.0047 - val_loss: 0.6607 - val_acc: 0.6429 - val_precision_14: 0.0000e+00 - val_recall_14: 0.0000e+00 Epoch 10/300 614/614 [==============================] - 0s 171us/sample - loss: 0.6463 - acc: 0.6547 - precision_14: 1.0000 - recall_14: 0.0047 - val_loss: 0.6594 - val_acc: 0.6429 - val_precision_14: 0.0000e+00 - val_recall_14: 0.0000e+00 Epoch 11/300 614/614 [==============================] - 0s 168us/sample - loss: 0.6445 - acc: 0.6547 - precision_14: 1.0000 - recall_14: 0.0047 - val_loss: 0.6575 - val_acc: 0.6429 - val_precision_14: 0.0000e+00 - val_recall_14: 0.0000e+00 Epoch 12/300 614/614 [==============================] - 0s 163us/sample - loss: 0.6422 - acc: 0.6547 - precision_14: 1.0000 - recall_14: 0.0047 - val_loss: 0.6547 - val_acc: 0.6429 - val_precision_14: 0.0000e+00 - val_recall_14: 0.0000e+00 Epoch 13/300 614/614 [==============================] - 0s 179us/sample - loss: 0.6407 - acc: 0.6547 - precision_14: 1.0000 - recall_14: 0.0047 - val_loss: 0.6524 - val_acc: 0.6494 - val_precision_14: 1.0000 - val_recall_14: 0.0182 Epoch 14/300 614/614 [==============================] - 0s 197us/sample - loss: 0.6382 - acc: 0.6547 - precision_14: 1.0000 - recall_14: 0.0047 - val_loss: 0.6510 - val_acc: 0.6494 - val_precision_14: 1.0000 - val_recall_14: 0.0182 Epoch 15/300 614/614 [==============================] - 0s 163us/sample - loss: 0.6362 - acc: 0.6564 - precision_14: 1.0000 - recall_14: 0.0094 - val_loss: 0.6487 - val_acc: 0.6494 - val_precision_14: 1.0000 - val_recall_14: 0.0182 Epoch 16/300 614/614 [==============================] - 0s 200us/sample - loss: 0.6340 - acc: 0.6564 - precision_14: 1.0000 - recall_14: 0.0094 - val_loss: 0.6464 - val_acc: 0.6429 - val_precision_14: 0.5000 - val_recall_14: 0.0182 Epoch 17/300 614/614 [==============================] - 0s 184us/sample - loss: 0.6319 - acc: 0.6547 - precision_14: 0.6667 - recall_14: 0.0094 - val_loss: 0.6443 - val_acc: 0.6429 - val_precision_14: 0.5000 - val_recall_14: 0.0182 Epoch 18/300 614/614 [==============================] - 0s 168us/sample - loss: 0.6301 - acc: 0.6547 - precision_14: 0.6667 - recall_14: 0.0094 - val_loss: 0.6426 - val_acc: 0.6494 - val_precision_14: 0.6667 - val_recall_14: 0.0364 Epoch 19/300 614/614 [==============================] - 0s 171us/sample - loss: 0.6278 - acc: 0.6547 - precision_14: 0.6667 - recall_14: 0.0094 - val_loss: 0.6410 - val_acc: 0.6429 - val_precision_14: 0.5000 - val_recall_14: 0.0364 Epoch 20/300 614/614 [==============================] - 0s 176us/sample - loss: 0.6257 - acc: 0.6547 - precision_14: 0.6667 - recall_14: 0.0094 - val_loss: 0.6390 - val_acc: 0.6429 - val_precision_14: 0.5000 - val_recall_14: 0.0364 … Epoch 281/300 614/614 [==============================] - 0s 211us/sample - loss: 0.4527 - acc: 0.7785 - precision_14: 0.7251 - recall_14: 0.5822 - val_loss: 0.4638 - val_acc: 0.8052 - val_precision_14: 0.7778 - val_recall_14: 0.6364 Epoch 282/300 614/614 [==============================] - 0s 166us/sample - loss: 0.4520 - acc: 0.7818 - precision_14: 0.7365 - recall_14: 0.5775 - val_loss: 0.4647 - val_acc: 0.8052 - val_precision_14: 0.7907 - val_recall_14: 0.6182 Epoch 283/300 614/614 [==============================] - 0s 169us/sample - loss: 0.4525 - acc: 0.7850 - precision_14: 0.7580 - recall_14: 0.5587 - val_loss: 0.4653 - val_acc: 0.7922 - val_precision_14: 0.7805 - val_recall_14: 0.5818 Epoch 284/300 614/614 [==============================] - 0s 197us/sample - loss: 0.4515 - acc: 0.7818 - precision_14: 0.7365 - recall_14: 0.5775 - val_loss: 0.4637 - val_acc: 0.8052 - val_precision_14: 0.7778 - val_recall_14: 0.6364 Epoch 285/300 614/614 [==============================] - 0s 176us/sample - loss: 0.4526 - acc: 0.7818 - precision_14: 0.7158 - recall_14: 0.6150 - val_loss: 0.4633 - val_acc: 0.7987 - val_precision_14: 0.7609 - val_recall_14: 0.6364 Epoch 286/300 614/614 [==============================] - 0s 210us/sample - loss: 0.4524 - acc: 0.7785 - precision_14: 0.7278 - recall_14: 0.5775 - val_loss: 0.4641 - val_acc: 0.8052 - val_precision_14: 0.7907 - val_recall_14: 0.6182 Epoch 287/300 614/614 [==============================] - 0s 176us/sample - loss: 0.4515 - acc: 0.7834 - precision_14: 0.7381 - recall_14: 0.5822 - val_loss: 0.4634 - val_acc: 0.8052 - val_precision_14: 0.7778 - val_recall_14: 0.6364 Epoch 288/300 614/614 [==============================] - 0s 176us/sample - loss: 0.4516 - acc: 0.7818 - precision_14: 0.7365 - recall_14: 0.5775 - val_loss: 0.4635 - val_acc: 0.7987 - val_precision_14: 0.7727 - val_recall_14: 0.6182 Epoch 289/300 614/614 [==============================] - 0s 178us/sample - loss: 0.4519 - acc: 0.7818 - precision_14: 0.7453 - recall_14: 0.5634 - val_loss: 0.4651 - val_acc: 0.7987 - val_precision_14: 0.7857 - val_recall_14: 0.6000 Epoch 290/300 614/614 [==============================] - 0s 180us/sample - loss: 0.4509 - acc: 0.7834 - precision_14: 0.7381 - recall_14: 0.5822 - val_loss: 0.4630 - val_acc: 0.8052 - val_precision_14: 0.7778 - val_recall_14: 0.6364 Epoch 291/300 614/614 [==============================] - 0s 197us/sample - loss: 0.4514 - acc: 0.7866 - precision_14: 0.7330 - recall_14: 0.6056 - val_loss: 0.4631 - val_acc: 0.8052 - val_precision_14: 0.7778 - val_recall_14: 0.6364 Epoch 292/300 614/614 [==============================] - 0s 124us/sample - loss: 0.4522 - acc: 0.7818 - precision_14: 0.7365 - recall_14: 0.5775 - val_loss: 0.4642 - val_acc: 0.8052 - val_precision_14: 0.7907 - val_recall_14: 0.6182 Epoch 293/300 614/614 [==============================] - 0s 134us/sample - loss: 0.4510 - acc: 0.7834 - precision_14: 0.7326 - recall_14: 0.5915 - val_loss: 0.4629 - val_acc: 0.8052 - val_precision_14: 0.7778 - val_recall_14: 0.6364 Epoch 294/300 614/614 [==============================] - 0s 141us/sample - loss: 0.4512 - acc: 0.7866 - precision_14: 0.7330 - recall_14: 0.6056 - val_loss: 0.4630 - val_acc: 0.8052 - val_precision_14: 0.7778 - val_recall_14: 0.6364 Epoch 295/300 614/614 [==============================] - 0s 176us/sample - loss: 0.4512 - acc: 0.7818 - precision_14: 0.7232 - recall_14: 0.6009 - val_loss: 0.4630 - val_acc: 0.8052 - val_precision_14: 0.7778 - val_recall_14: 0.6364 Epoch 296/300 614/614 [==============================] - 0s 166us/sample - loss: 0.4510 - acc: 0.7834 - precision_14: 0.7326 - recall_14: 0.5915 - val_loss: 0.4637 - val_acc: 0.7987 - val_precision_14: 0.7727 - val_recall_14: 0.6182 Epoch 297/300 614/614 [==============================] - 0s 189us/sample - loss: 0.4509 - acc: 0.7834 - precision_14: 0.7299 - recall_14: 0.5962 - val_loss: 0.4633 - val_acc: 0.8052 - val_precision_14: 0.7778 - val_recall_14: 0.6364 Epoch 298/300 614/614 [==============================] - 0s 139us/sample - loss: 0.4511 - acc: 0.7801 - precision_14: 0.7294 - recall_14: 0.5822 - val_loss: 0.4633 - val_acc: 0.8052 - val_precision_14: 0.7778 - val_recall_14: 0.6364 Epoch 299/300 614/614 [==============================] - 0s 172us/sample - loss: 0.4533 - acc: 0.7801 - precision_14: 0.7143 - recall_14: 0.6103 - val_loss: 0.4629 - val_acc: 0.7987 - val_precision_14: 0.7609 - val_recall_14: 0.6364 Epoch 300/300 614/614 [==============================] - 0s 181us/sample - loss: 0.4509 - acc: 0.7850 - precision_14: 0.7425 - recall_14: 0.5822 - val_loss: 0.4638 - val_acc: 0.8052 - val_precision_14: 0.7907 - val_recall_14: 0.6182
As seen above, at the end of the 300th epoch, the model had a loss of 45.09%, an accuracy of 78.50%, precision of 74.25%, and a recall of 58.22%. This is a pretty decent result with a very simple neural network.
Let’s visualize how the training process went.
#plot the loss and validation loss of the dataset history_df = pd.DataFrame(history.history) plt.plot(history_df['loss'], label='loss') plt.plot(history_df['val_loss'], label='val_loss') plt.legend()
Output:
Adding Some Hidden Layers (a Multilayer Perceptron)
Let’s tweak the neural network architecture by adding more layers with some dropout and see how the performance will be affected.
This time, the first hidden layer has 16 nodes with a ReLu activation function. In the next layer, the nodes were reduced to 12, with a 20% dropout to avoid overfitting. The next layer had 3 nodes with a ReLu activation while the final layer was a single-node layer with the sigmoid activation.
The optimizer, metrics and loss function remains the same as in the last architecture.
def create_model(): '''The function creates a Perceptron using Keras''' model = Sequential() model.add(Dense(16, input_dim=len(X.columns), activation='relu')) model.add(Dense(12, activation='relu')) model.add(Dropout(0.2)) model.add(Dense(3, activation='relu')) model.add(Dense(1, activation='sigmoid')) return model import tensorflow as tf estimator = create_model() estimator.compile(optimizer='adam', metrics=['accuracy', tf.keras.metrics.Precision(), tf.keras.metrics.Recall()], loss='binary_crossentropy')
Now, we train the model on 300 epochs as well.
#train the model history = estimator.fit(X_train, y_train, epochs=300, validation_data=(X_test, y_test))
Output:
Train on 614 samples, validate on 154 samples Epoch 1/300 614/614 [==============================] - 2s 4ms/sample - loss: 0.7018 - acc: 0.4235 - precision_17: 0.3667 - recall_17: 0.9108 - val_loss: 0.6878 - val_acc: 0.7338 - val_precision_17: 0.6591 - val_recall_17: 0.5273 Epoch 2/300 614/614 [==============================] - 0s 156us/sample - loss: 0.6924 - acc: 0.5749 - precision_17: 0.4172 - recall_17: 0.5681 - val_loss: 0.6855 - val_acc: 0.6883 - val_precision_17: 0.6842 - val_recall_17: 0.2364 Epoch 3/300 614/614 [==============================] - 0s 175us/sample - loss: 0.6883 - acc: 0.6173 - precision_17: 0.4505 - recall_17: 0.4695 - val_loss: 0.6831 - val_acc: 0.6948 - val_precision_17: 0.7500 - val_recall_17: 0.2182 Epoch 4/300 614/614 [==============================] - 0s 173us/sample - loss: 0.6842 - acc: 0.6564 - precision_17: 0.5079 - recall_17: 0.3005 - val_loss: 0.6809 - val_acc: 0.6623 - val_precision_17: 0.8000 - val_recall_17: 0.0727 Epoch 5/300 614/614 [==============================] - 0s 188us/sample - loss: 0.6799 - acc: 0.6775 - precision_17: 0.5882 - recall_17: 0.2347 - val_loss: 0.6784 - val_acc: 0.6558 - val_precision_17: 0.6667 - val_recall_17: 0.0727 Epoch 6/300 614/614 [==============================] - 0s 191us/sample - loss: 0.6771 - acc: 0.6808 - precision_17: 0.6049 - recall_17: 0.2300 - val_loss: 0.6758 - val_acc: 0.6623 - val_precision_17: 0.7143 - val_recall_17: 0.0909 Epoch 7/300 614/614 [==============================] - 0s 221us/sample - loss: 0.6752 - acc: 0.6775 - precision_17: 0.6087 - recall_17: 0.1972 - val_loss: 0.6737 - val_acc: 0.6623 - val_precision_17: 0.8000 - val_recall_17: 0.0727 Epoch 8/300 614/614 [==============================] - 0s 210us/sample - loss: 0.6731 - acc: 0.6759 - precision_17: 0.6522 - recall_17: 0.1408 - val_loss: 0.6715 - val_acc: 0.6558 - val_precision_17: 1.0000 - val_recall_17: 0.0364 Epoch 9/300 614/614 [==============================] - 0s 170us/sample - loss: 0.6699 - acc: 0.6645 - precision_17: 0.6000 - recall_17: 0.0986 - val_loss: 0.6690 - val_acc: 0.6623 - val_precision_17: 0.8000 - val_recall_17: 0.0727 Epoch 10/300 614/614 [==============================] - 0s 189us/sample - loss: 0.6675 - acc: 0.6824 - precision_17: 0.6667 - recall_17: 0.1690 - val_loss: 0.6663 - val_acc: 0.6753 - val_precision_17: 0.7778 - val_recall_17: 0.1273 Epoch 11/300 614/614 [==============================] - 0s 184us/sample - loss: 0.6643 - acc: 0.6889 - precision_17: 0.7115 - recall_17: 0.1737 - val_loss: 0.6643 - val_acc: 0.6623 - val_precision_17: 1.0000 - val_recall_17: 0.0545 Epoch 12/300 614/614 [==============================] - 0s 170us/sample - loss: 0.6628 - acc: 0.6661 - precision_17: 0.5870 - recall_17: 0.1268 - val_loss: 0.6617 - val_acc: 0.6753 - val_precision_17: 0.8571 - val_recall_17: 0.1091 Epoch 13/300 614/614 [==============================] - 0s 166us/sample - loss: 0.6595 - acc: 0.7003 - precision_17: 0.7164 - recall_17: 0.2254 - val_loss: 0.6589 - val_acc: 0.6818 - val_precision_17: 0.8750 - val_recall_17: 0.1273 Epoch 14/300 614/614 [==============================] - 0s 163us/sample - loss: 0.6553 - acc: 0.6938 - precision_17: 0.7451 - recall_17: 0.1784 - val_loss: 0.6562 - val_acc: 0.6818 - val_precision_17: 0.8750 - val_recall_17: 0.1273 Epoch 15/300 614/614 [==============================] - 0s 164us/sample - loss: 0.6560 - acc: 0.6873 - precision_17: 0.6842 - recall_17: 0.1831 - val_loss: 0.6532 - val_acc: 0.6948 - val_precision_17: 0.9000 - val_recall_17: 0.1636 Epoch 16/300 614/614 [==============================] - 0s 168us/sample - loss: 0.6521 - acc: 0.7003 - precision_17: 0.7042 - recall_17: 0.2347 - val_loss: 0.6508 - val_acc: 0.6948 - val_precision_17: 0.9000 - val_recall_17: 0.1636 Epoch 17/300 614/614 [==============================] - 0s 178us/sample - loss: 0.6506 - acc: 0.6840 - precision_17: 0.6727 - recall_17: 0.1737 - val_loss: 0.6478 - val_acc: 0.7013 - val_precision_17: 0.9091 - val_recall_17: 0.1818 Epoch 18/300 614/614 [==============================] - 0s 163us/sample - loss: 0.6425 - acc: 0.7036 - precision_17: 0.6914 - recall_17: 0.2629 - val_loss: 0.6452 - val_acc: 0.7468 - val_precision_17: 0.7667 - val_recall_17: 0.4182 Epoch 19/300 614/614 [==============================] - 0s 179us/sample - loss: 0.6465 - acc: 0.7215 - precision_17: 0.6458 - recall_17: 0.4366 - val_loss: 0.6408 - val_acc: 0.7208 - val_precision_17: 0.8333 - val_recall_17: 0.2727 Epoch 20/300 614/614 [==============================] - 0s 158us/sample - loss: 0.6365 - acc: 0.7264 - precision_17: 0.7528 - recall_17: 0.3146 - val_loss: 0.6375 - val_acc: 0.7468 - val_precision_17: 0.7500 - val_recall_17: 0.4364 … Epoch 281/300 614/614 [==============================] - 0s 197us/sample - loss: 0.4374 - acc: 0.7883 - precision_17: 0.7862 - recall_17: 0.5352 - val_loss: 0.4249 - val_acc: 0.7857 - val_precision_17: 0.7500 - val_recall_17: 0.6000 Epoch 282/300 614/614 [==============================] - 0s 203us/sample - loss: 0.4210 - acc: 0.8127 - precision_17: 0.7882 - recall_17: 0.6291 - val_loss: 0.4293 - val_acc: 0.7792 - val_precision_17: 0.7442 - val_recall_17: 0.5818 Epoch 283/300 614/614 [==============================] - 0s 200us/sample - loss: 0.4402 - acc: 0.7850 - precision_17: 0.7718 - recall_17: 0.5399 - val_loss: 0.4301 - val_acc: 0.7987 - val_precision_17: 0.7857 - val_recall_17: 0.6000 Epoch 284/300 614/614 [==============================] - 0s 207us/sample - loss: 0.4354 - acc: 0.8208 - precision_17: 0.8084 - recall_17: 0.6338 - val_loss: 0.4280 - val_acc: 0.7857 - val_precision_17: 0.7391 - val_recall_17: 0.6182 Epoch 285/300 614/614 [==============================] - 0s 200us/sample - loss: 0.4444 - acc: 0.7915 - precision_17: 0.7673 - recall_17: 0.5728 - val_loss: 0.4310 - val_acc: 0.7922 - val_precision_17: 0.7805 - val_recall_17: 0.5818 Epoch 286/300 614/614 [==============================] - 0s 220us/sample - loss: 0.4380 - acc: 0.8046 - precision_17: 0.7888 - recall_17: 0.5962 - val_loss: 0.4315 - val_acc: 0.7727 - val_precision_17: 0.7381 - val_recall_17: 0.5636 Epoch 287/300 614/614 [==============================] - 0s 208us/sample - loss: 0.4297 - acc: 0.8013 - precision_17: 0.7725 - recall_17: 0.6056 - val_loss: 0.4278 - val_acc: 0.8052 - val_precision_17: 0.7660 - val_recall_17: 0.6545 Epoch 288/300 614/614 [==============================] - 0s 192us/sample - loss: 0.4266 - acc: 0.8062 - precision_17: 0.8013 - recall_17: 0.5869 - val_loss: 0.4295 - val_acc: 0.7857 - val_precision_17: 0.7500 - val_recall_17: 0.6000 Epoch 289/300 614/614 [==============================] - 0s 163us/sample - loss: 0.4294 - acc: 0.8078 - precision_17: 0.7987 - recall_17: 0.5962 - val_loss: 0.4298 - val_acc: 0.7922 - val_precision_17: 0.7556 - val_recall_17: 0.6182 Epoch 290/300 614/614 [==============================] - 0s 192us/sample - loss: 0.4299 - acc: 0.8094 - precision_17: 0.7667 - recall_17: 0.6479 - val_loss: 0.4346 - val_acc: 0.7857 - val_precision_17: 0.7750 - val_recall_17: 0.5636 Epoch 291/300 614/614 [==============================] - 0s 193us/sample - loss: 0.4333 - acc: 0.8094 - precision_17: 0.7824 - recall_17: 0.6244 - val_loss: 0.4301 - val_acc: 0.7987 - val_precision_17: 0.7727 - val_recall_17: 0.6182 Epoch 292/300 614/614 [==============================] - 0s 263us/sample - loss: 0.4380 - acc: 0.8029 - precision_17: 0.7674 - recall_17: 0.6197 - val_loss: 0.4278 - val_acc: 0.7922 - val_precision_17: 0.7556 - val_recall_17: 0.6182 Epoch 293/300 614/614 [==============================] - 0s 206us/sample - loss: 0.4212 - acc: 0.8127 - precision_17: 0.7816 - recall_17: 0.6385 - val_loss: 0.4263 - val_acc: 0.7987 - val_precision_17: 0.7609 - val_recall_17: 0.6364 Epoch 294/300 614/614 [==============================] - 0s 185us/sample - loss: 0.4322 - acc: 0.8078 - precision_17: 0.7844 - recall_17: 0.6150 - val_loss: 0.4293 - val_acc: 0.7922 - val_precision_17: 0.7674 - val_recall_17: 0.6000 Epoch 295/300 614/614 [==============================] - 0s 243us/sample - loss: 0.4377 - acc: 0.8046 - precision_17: 0.7784 - recall_17: 0.6103 - val_loss: 0.4298 - val_acc: 0.7922 - val_precision_17: 0.7556 - val_recall_17: 0.6182 Epoch 296/300 614/614 [==============================] - 0s 217us/sample - loss: 0.4348 - acc: 0.7866 - precision_17: 0.7563 - recall_17: 0.5681 - val_loss: 0.4308 - val_acc: 0.7857 - val_precision_17: 0.7500 - val_recall_17: 0.6000 Epoch 297/300 614/614 [==============================] - 0s 180us/sample - loss: 0.4295 - acc: 0.7997 - precision_17: 0.7557 - recall_17: 0.6244 - val_loss: 0.4287 - val_acc: 0.7857 - val_precision_17: 0.7619 - val_recall_17: 0.5818 Epoch 298/300 614/614 [==============================] - 0s 200us/sample - loss: 0.4431 - acc: 0.7915 - precision_17: 0.7607 - recall_17: 0.5822 - val_loss: 0.4296 - val_acc: 0.7857 - val_precision_17: 0.7500 - val_recall_17: 0.6000 Epoch 299/300 614/614 [==============================] - 0s 167us/sample - loss: 0.4310 - acc: 0.8046 - precision_17: 0.7853 - recall_17: 0.6009 - val_loss: 0.4296 - val_acc: 0.7792 - val_precision_17: 0.7442 - val_recall_17: 0.5818 Epoch 300/300 614/614 [==============================] - 0s 178us/sample - loss: 0.4190 - acc: 0.8078 - precision_17: 0.7684 - recall_17: 0.6385 - val_loss: 0.4269 - val_acc: 0.7857 - val_precision_17: 0.7500 - val_recall_17: 0.6000
This time, the model has a loss of 41.9%, an accuracy of 80.78%, precision of 76.84%, and a recall of 63.85. These results are slightly better than the previous model but are not convincing.
It goes to show that for this dataset, increasing the number of layers does not necessarily improve the performance of the model.
Finally, we can visualize the training process with the code below.
#plot the loss and validation loss of the dataset history_df = pd.DataFrame(history.history) plt.plot(history_df['loss'], label='loss') plt.plot(history_df['val_loss'], label='val_loss') plt.legend()
Output:
Summary
In conclusion, you have discovered how to build a binary classifier using Keras. We started out by carrying out some EDA after which the data was preprocessed and then fed into the neural network. For this dataset, we found out that increasing the number of hidden layers in the neural network architecture does not have a significant effect on the performance of the model.
You can conclude that this is because the dataset was a relatively small dataset. It explains why a single perceptron was able to capture the patterns in the data with an accuracy of over 80%.






























One Response