Java Variables and Data Types

Variable is a name associated with a piece of memory that stores data and whose associated value may be changed  To declare a variable you need to write the Java variable type with giving it a name. 

For example, let’s declare two variables. One is named  personName and has type String, other is named personAge and is of type int.

String personName;
int personAge;       

Now that we’ve declared a variable, we can give it a value. This is called initializing a variable. To initialize a variable, you just type the variable name followed by an equal sign, followed by the desired value:

personName = “Denis”;
personAge = 30;

Since you often want to initialize a variable right away, you can do so in the same statement as the declaration. For example, here we merge the previous declarations and initializations into more concise code:

String personName = “Denis”;
int personAge = 30;

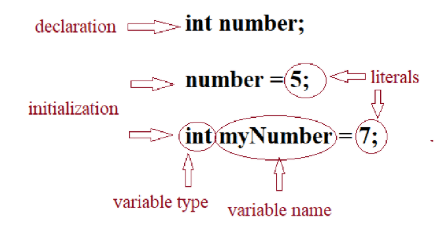
In the picture below you can find basic terms that developers use for variables:

You can also declare and initialize multiple variables in the same statement. How many variables do you think are declared and initialized in the following two lines?

String str1, str2;
String str3 = “yes”, str4 = “no”;

We declared 4 String variables were declared: str1, str2, str3, and str4. You can declare many variables in the same declaration in case they have the same type. You can also initialize any or all of those values inline. In the previous example, we have two initialized variables: str3 and str4. The other two variables remain declared but not initialized.

Pay attention to tricky things! This is where it gets tricky. 

Let’s try one more example, how many variables do you think are declared and initialized in this code?

int i1, i2, i3 = 0;

As you should expect, 3 variables were declared: i1, i2, and i3. If you look with the attention you will understand that only one of those values i3 was initialized. The other two are declared but not initialized.

That’s the trick. Each snippet separated by a comma is a little declaration of its own. The initialization of i3 only applies to i3. It doesn’t have anything to do with i1 or i2 despite being in the same statement.

Look at this line:

int num, String value; // DOES NOT COMPILE

This code doesn’t compile because it tries to declare multiple variables of different types in the same statement. The shortcut to declare multiple variables in the same statement only works when they share a type.

To make sure you understand this, see if you can figure out which of the following are legal declarations:

boolean b1, b2;
String s1 = “1”, s2;
double d1, double d2;
int i1; int i2;
int i3; i4;

The first statement declares two variables without initializing them. The second statement declares two variables and initializes only one of them. Look at the third statement. It is not legal. Java does not allow you to declare two different types in the same statement. Variables d1 and d2 are the same types. They are both of type double. Although that’s true, it still isn’t allowed. If you want to declare multiple variables in the same statement, they must share the same type declaration and not repeat

1. double d1, d2; would have been legal.

The fourth statement is legal. Although int does appear twice, each one is in a separate statement. A semicolon (;) separates statements in Java. It just so happens there are two completely different statements on the same line. The fifth statement is not legal. Again, we have two completely different statements on the same line. The second one is not a valid declaration because it omits the type. When you see an oddly placed semicolon on the exam, pretend the code is on separate lines and think about whether the code compiles that way. In this case, we have the following:

int i1;
int i2;
int i3;
i4;// DOES NOT COMPILE

Looking at the last line on its own, you can easily see that the declaration is invalid. And yes, the exam really does cram multiple statements onto the same line partly to try to trick you and partly to fit more code on the screen. In the real world, please limit yourself to one declaration per statement and line. Your teammates will thank you for the readable code.

Identifiers

Java has rules about identifier names. The same rules for identifiers apply to variables, methods, classes, and fields.

The rules are:

• The identifier must begin with a letter or the symbol $ or _.
• Subsequent characters in the name may also be numbers.
• A reserved word is a keyword that Java has reserved so that you are not allowed to use it. You cannot use the same name as a Java reserved word.

Java is case sensitive, so you can use versions of the keywords that only differ in case. 

These examples are not legal:

3DPointIdentifier // identifiers cannot begin with a number

hello@identifier // @ is not a letter, digit, $ or _
*$mycoffee // * is not a letter, digit, $ or _
public // public is a reserved word 

 

The following examples are legal:

okidentifier

$OK5Identifier
_alsoOK8d2ntifi3r

There are also code conventions for identifier names:

• In Java methods and variables names have to start from a lowercase letter followed by CamelCase.
• Class names have to begin with an uppercase letter followed by CamelCase. The compiler uses this symbol $ for some files. Don’t start any identifiers with $. 

Understanding Default Initialization of Variables

Before you start using a variable, it needs a value. Some types of variables are getting value automatically, some require the programmer to specify it. 

 A local variable is defined within a method and must be initialized before use. They do not have a default value and contain garbage data.  Not local variables are called instance or class variables. Instance variables are also called fields. Class variables can be shared across several objects. Instance and class variables do not require to be initialized. When you declare these variables, they are given a default value.

 

Data Types

There are two types of data in Java: primitive types and reference types. 

Java has eight built-in data types, referred to as the Java primitive types. The table below shows the Java primitive types together with their size in bytes and the range of values that each holds.

 

Keyword	Type	Example
boolean	True or false	true
byte	8-bit integral value	123
short	16-bit integral value	123
int	32-bit integral value	123
long	64-bit integral value	123
float	32-bit floating-point value	123.45f
double	64-bit floating-point value	123.456
char	16-bit Unicode value	‘a’

Here are key points about types:

• for floating-point values float and double types are used.
• a float type must have the letter f following the number.
• for numbers without decimal points byte, short, int, and long types are used.

Let’s talk a bit more about numeric primitives. When a number is present in the code, it is called a literal.  Java assumes you are defining an int value with a literal. Look at the example below, the number listed is bigger and does not fit in an int type. There is a possibility to get maximum value for an int.

long max = 3923656245789; // DOES NOT COMPILE

 

Java compiler will complain that the number is out of range. But it is for an int. However, we don’t have an int. To fix the problem we need to add the character L to the number:

 

long max = 3123456789L; // it is a long

Also, you could add a lowercase l to the number, but better is to use the uppercase L. The lowercase l looks similar to the number 1.

Primitive Data types hold values in the memory where the variable is allocated, references do not hold the value of the object they refer to.  Reference type points to an instance of a class by storing the memory address where the object is located, a concept referred to as a pointer. Unlike other languages, Java does not allow you to learn what the physical memory address is. You can only use the reference to refer to the object.

Reference types in Java: class types (this reference type points to an object of a class), array types (this reference type points to an array), interface types (this reference type points to an object of a class which implements an interface).

Here are examples that declare and initialize reference types. We declare a reference of type java.util.Date and a reference of type String:

java.util.Date today;
String greeting;

The today variable is a reference of type Date and can only point to a Date object. The greeting variable is a reference that can only point to a String object. A value is assigned to a reference in one of two ways:

• A reference can be assigned to another object of the same type.
• A reference can be assigned to a new object using the new keyword.

For example, the following statements assign these references to new objects:

today = new java.util.Date();
greeting = “How are you?”;

Today reference now points to a new Date object in memory, and today can be used to access the various fields and methods of this Date object. Similarly, the greeting reference points to a new String object, “How are you?”. The String and Date objects do not have names and can be accessed only via their corresponding reference.